5.5.2.1　理论基础和方法

人们对于时间序列的研究已有数十年的历史了，但主要集中在线性方面的研究。近年来，对非线性系统尤其是混沌背景下产生的时间序列的分析越来越受到重视。混沌现象介于确定性与随机性之间，是自然界中客观存在的一类现象。一方面，在一个确定性系统中，混沌现象对初始条件非常敏感，一个小小的扰动变化可能被放大，产生意想不到的结果，使混沌运动具有长期不可预测的特性；另一方面，混沌现象蕴含着有序，它不同于无从控制的随机运动，轨迹发散但逃逸不出奇异吸引子的约束，这使得进行短期预测是可行的，且比利用传统的线性预测模型所获得的结果要好。

混沌时间序列预测的理论基础是状态空间的重构理论，即把具有混沌特性的时间序列重建为一种低阶、非线性动力学系统。通过相空间重构，可以找出隐藏在混沌吸引子中的演化规律，使现有的数据纳入某种可描述的框架之下，从而为时间序列的研究提供了一种崭新的方法和思路。相空间重构是非线性时间序列分析的重要步骤，重构的质量直接影响到所建模型及其预测的质量。延迟时间和嵌入维数的选择是相空间重构的两个重要参数。

假设在某系统中，唯一可观察到的是单变量时间序列｛X（ti）｝，为研究其动力学模型，需重构相空间。显然，该时间序列的过去状态含有现在状态的信息，该信息可以表示为维数为m的时延向量

式中：m为嵌入维数；τ为延迟时间。

利用过去的经历构造状态是时间序列分析的一种标准方法。经过相空间重构，如分数维、Lyapunov指数等一些不变量可得到保留。

1.延迟时间τ的确定

当τ的选择过小时，x（t）和x（t＋τ）在数值上彼此接近，因此不能相互独立。而当τ过大时，就混沌吸引子而言，由于蝴蝶效应的影响，x（t）和x（t＋τ）相互之间的关系就变成随机了。因此，需要一种方法来选择恰当的τ，使得x（t）和x（t＋τ）之间既相互独立，又不至于在统计意义上完全无关，此可用如下两种方法来确定。

（1）自关联函数法。设样本集xi＝x（t0＋iτs），其中τs是样本的取值时间，则xi的自关联函数定义为：

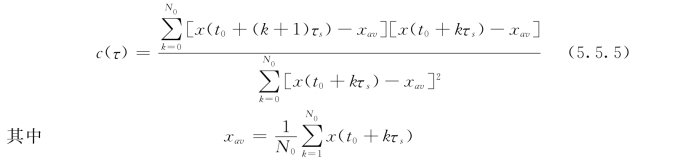
可取使c（τ）首次通过零点时的τ为延迟时间，因为此时是使x（t）为线性无关的最小值。

（2）周期轨道法。通过大量计算和对已知系统的数值试验，认为当取τ＝T/4为延迟时间时，可接近最佳重构，其中T 为混沌轨道近似周期。时间域采样定理表明，若x（t）为单值、频带宽度有限的时间函数，则当采样间隔τ≤T/2时，即可精确的复现x（t）。混沌吸引子虽无周期而言，但其具有半稳定的周期轨道。寻找合适的相点xi（t），依次计算它与xi＋1（t），xi＋2（t），…之间的距离，直到找到一个xk（t），使得与xi（t）的距离ρ［xk（t）－xi（t）］＜ε。从xi（t）到xk（t）的轨道就是一个周期轨道，我们可以将从xi（t）到xk（t）所用的平均时间当作周期T。因此认为，取延迟时间τ＝T/4是在不过分减少信息损失的前提下做出的合理选择。

2.嵌入维数m 的确定

要重构相空间，首先要找到相空间的维数，维数是空间和客体的重要几何参量。吸引子的维数说明了刻画该吸引子所必须的信息量，描述了该动力系统的复杂程度或系统的自由度。一个处于混沌状态的非线性系统，其相空间的运动轨迹是十分复杂的，对初始条件极为敏感，具有非整数维—分维特性，这种吸引子称为奇异吸引子。计算分维数的方法有：Hausdroff维、自相似维、Kolomogrov容量维、信息维和关联维数等（孙海云等，2000）。由于关联维数仅凭借系统的观测数据序列就可以得到关于吸引子维数的信息，因此使用较普遍。

有关求解嵌入维数m的数学表达式，见第四章中的相关公式（4.4.3）～（4.4.7）。

3.Lyapunov指数的预报模式

Lyapunov指数作为量化对初始轨道的指数发散和估计系统混沌水平的特征量，是系统的一个很好的预报参数。从一维时间序列中获取Lyapunov指数值，一般包括如下步骤。

1）应用时间序列选取延迟时间τ，根据观测数据样本总数N，构造n 维相空间的新序列，相点数为m：m＝N－（n－1）τ。

2）以初始相点x0为基点，在点集｛xi｝的其余相点中选取与x0最近的点xj为端点，构成一初始向量，x0～xj间欧氏距离可记为L（t0）。

3）取时间步长为k，t1＝t0＋k，初始向量沿轨线向前演化得到一新向量，其相应基点与端点间欧氏距离可记为L（t1）。在相应时间段内系统线度指数增长率记为(www.daowen.com)

4）如此继续直至所有相点，然后取各指数增长率的平均值即为最大Lyapunov指数估计值

5）依次增加嵌入维数m，重复2）、3）、4）过程直至Lyapunov指数估计值随n变化而变得较为平稳为止，此时得到的计算结果即为所求的最大Lyapunov指数值。

关于一维Lyapunov指数预测模式，不妨设xm为预报的中心点，相空间xm的最邻近的点为xk，其距离为

若最大Lyapunov指数为LE1，则

式中：点xm＋1只有最后一个分量x（tn＋1）未知，故x（tn＋1）是可以预报的。

一般地，定义最长预报时间为：Tm＝1/LE1。它表示系统状态误差增加一倍所需要的最长时间。

5.5.2.2　相空间重构的预测模型的VB实现

通过Matlab6.1 语言编程计算，经拟合可分别求出各曲线的斜率，并分别得到各关联维数D 的估计值。对应于一个嵌入维数m 就可得出相应一个关联维数D 的估计值；将所有的（m，D）的组值进行作图（见图5.5.2），达到饱和（即基本不再变化）时为止。

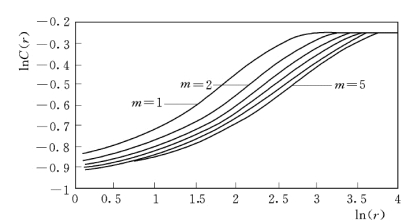
图5.5.2　lnC（r）—lnr的变化关系

图5.5.2显示，lnC（r）—lnr 曲线上有一段呈良好的线性关系。当嵌入维数m较小时，曲线的直线部分的斜率（关联维数D）较小，彼此之间的间隔较大；随着嵌入维数m 的增加，直线部分的斜率逐渐增大，其间隔变小，且逐渐靠拢；当m 达到一定值时，相关直线密集且互相间趋于平行。此表明，其斜率不再随嵌入维数m的增大而发生很大变化，即有D2（mc）＝D2（mc＋1）＝D2（mc＋2）＝…。

图5.5.3 显示，当嵌入维数m增大到5 时，D2（m）已经达到了饱和值，相应地可以得出曲线的直线部分的斜率趋于稳定值。该值D2＝1.68 为非整数，表示存在吸引子，说明相应的观测资料时间序列为一混沌系统，即系统呈现混沌。基于相空间重构理论的建模流程见图5.5.4。

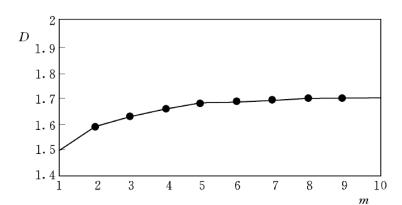
图5.5.3　D 与m 的变化关系

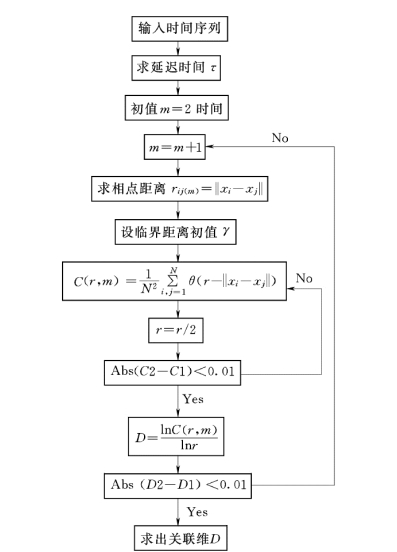
图5.5.4　基于相空间重构理论模型的流程图