ARIMA（Autoregressive integrated moving average）模型指自回归求和移动平均模型，可分为非季节性和季节性两种（Peter 等，2001）。非季节性ARIMA模型，是BoxJenkons方法中重要的预测模型，适于处理非平稳时间序列。其建模的基本思路：通过某资料系列的过去值和过去误差、或当前值和过去值的线性组合，实现建模并进行趋势预测；对于非平稳时间序列，可用若干次差分（称之为“求和”）使其成为平稳序列。此为自回归移动平均即ARMA（Autoregressive moving average）过程。

ARIMA模型为自回归（AR）模型和移动平均（MA）模型的组合模型。若AR和MA的阶数分别为p 和q，差分的次数为d，则非季节性ARIMA模型可写作ARIMA（p，d，q）。即

可简写为

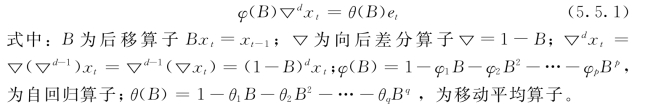
上述模型中需要确定的参数有φ1，φ2，…，φp和θ1，θ2，…，θq。显然，阶数越高，模型中待定的参数就越多。

季节性ARIMA模型其建模过程与非季节性ARIMA模型建模过程相同，只是在对时间点进行预测时考虑了季节性周期变化的因素。对于呈季节性或周期性变化的时间系列，季节性ARIMA模型尤为适用。用Sp、Sq 分别表示季节性自回归、季节性移动平均的阶数，Sd 表示季节性差分的次数，其一般可表示为ARIMA（Sp，Sd，Sq）s，即

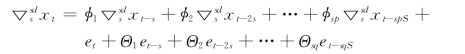
可简写为

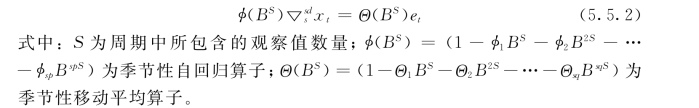
模型中需要确定的参数有Φ1，Φ2，…，Φsp和Θ1，Θ2，…，Θsq。

通常，呈季节性变化的时间序列不仅包含有季节性变化的分量，还包含有非季节性变化的分量。或者说，研究者不仅关心不同周期间观察值的变化情况，还关心同一周期内观察值的变化情况。这时可用ARIMA乘积模型进行趋势预测(www.daowen.com)

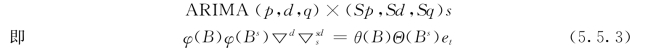
ARIMA模型的建立过程通常包括如下步骤。

（1）根据预测目标，建立平稳时间序列，并初步选定预测模型的基本形式。在对数据进行平稳化处理中，如果数据序列存在一定的趋势（如增长趋势或下降趋势等），需对数据进行差分处理；如果数据序列存在异常的方差，则需对数据进行对数变换，直至处理后数据的自相关函数值有趋于零的趋势。

（2）模型识别。采用自相关分析、偏自相关分析法从AR（p）、MA（q）、ARMA（p，q）和ARIMA（p，d，q）等模型中选择一个作为建模用的模型结构，并确定模型的阶次。

（3）参数估计。结合选定的试验模型，进行模型参数和阶次的估计，确定预测模型，并采用极大似然估计法得到模型中待求参数的估计值。从参数估计值的显著性检验（包括参数估计值、标准误差、T 统计量、检验概率P 等），判定模型中的一些项是否需要；从拟合优度统计量检验（包括残差序列的方差、方差估计值的平方根、AIC、BIC 统计量等），比较该模型和其他模型之间的优劣；从参数估计值的相关系数检验（包括自相关系数、偏自相关系数、逆自相关系数等），判断参数互线性可能影响的程度。如果两个参数估计值高度相关，可以考虑从模型中去掉一个；根据残差序列的卡方统计量检验，判定残差是否相关或包含可以被更复杂模型采用的额外信息。

（4）模型检验。此可通过对原时间序列与所建模型之间的误差序列是否具有随机性的检验来实现。若模型检验不能通过，则需回到上述步骤（2）重新进行模型结构辨识，直至合适为止；如果合适，则可用于预测。

（5）模型预测。利用所建模型进行预测，有关ARIMA模型的建模过程见图5.5.1。

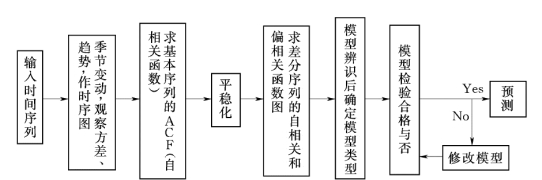
图5.5.1　ARIMA模型建模流程图

已有的研究表明（张蔚等，2002），ARIMA模型可以处理多种数据类型（包括含有趋势性、季节性和随机性等），而那些具有动态性、随机性和时变性的问题，在统计上均具有完善性，并有牢固的数学理论基础。尽管该模型由于其综合性和复杂性带来了计算上的困难，但由于信息技术和计算机技术的广泛应用而可以得到解决，因此该模型的应用得到了关注和重视。