这里，仍以水东大坝基础廊道Up07孔位扬压力的分析为例，探讨BP模型求解此类问题的有效性。有关研究区具体的地质及水文地质条件见4.6.1.1节。

根据Up07 孔扬压力原型观测资料，经逐步回归分析筛选得到如下因子：水压因子（H）；温度因子（cos2πt/365、sin2πt/365 cos4πt/365、sin4πt/365）；时效因子（lnt）。依据4.3节所述的基本原理和方法，建立了反映扬压力与上述影响因子之间关系的BP网络模型。该模型中不同层结点数，输入层为6，输出层为1，隐含层为10。采用Levenberg Marquardt算法训练网络，输入层和隐含层之间的连接权值、隐含层和输出层之间的连接权值见表4.6.4。

表4.6.4　实例中BP网络训练的权值统计

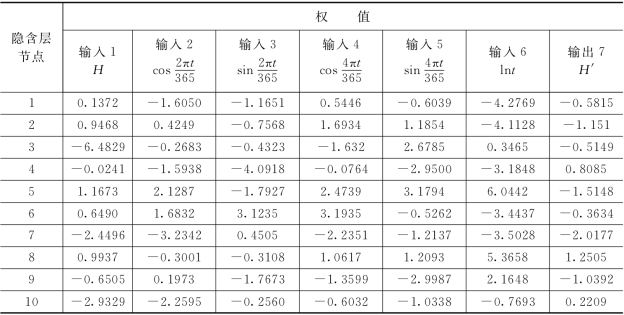
注　表中H′为扬压力水头。

经过计算，得到各因子对输出的影响比例，见表4.6.5。可知，该孔位扬压力的变化主要受上游库水位的影响，时效的影响次之，温度的影响则最小，而与统计模型的计算结果（表4.6.3）基本一致。但从残差过程线（图4.6.7）可以得出，神经网络模型的计算精度明显高于统计模型。(www.daowen.com)

表4.6.5　BP模型中扬压力各影响分量统计

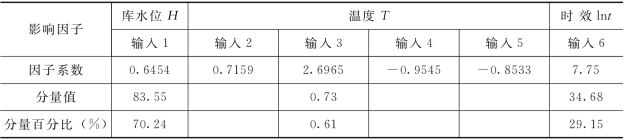
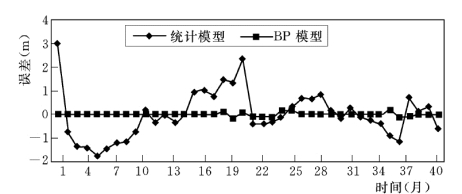
图4.6.7　不同模型残差过程线比较

在上述实例中，还尝试用权植反传法来量化影响坝基扬压力变化的有关因子，发现在对网络训练达到一定次数后很快收敛。计算结果表明，应用上述模型在进行非线性多变量的拟合方面有着显著的优点，即不必事先建立数学模型，用环境量去拟合效应量，其拟合结果的精度高于常规的统计模型。因而认为，对于需要定量分析环境量对效应量的影响程度方面的一类问题，应用神经网络模型具有较好的前景。