4.5.1.1　数据处理

GM建模时，需采取一定的方式对原始数据进行生成处理，使生成数据序列变成有规则序列。这样做，旨在：①为建模提供中间信息；②弱化原随机序列的随机性。

累加生成（Accumulated Generating Operation，简称AGO），即对原始数列中各时刻的数据依次累加，从而形成新的序列。设原始数列为

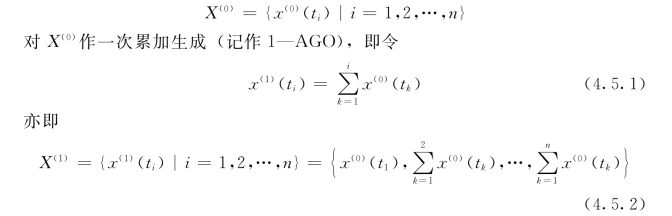
若对X（0）作m次累加生成（记作m—AGO），则有

一般地，随着对非负数列累加生成次数的增加，数列的随机性趋于弱化；当累加生成次数足够多时，该序列便由随机序列转变为非随机序列了。在GM模型中，一般只对数列作1 次累加生成（1—AGO）。

累减生成（Inverse Accumulated Generating Operation，简称IAGO）是AGO的逆运算，即对序列中前、后两数据进行差值运算。

令

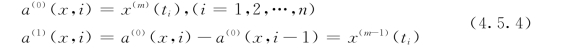
相应地有

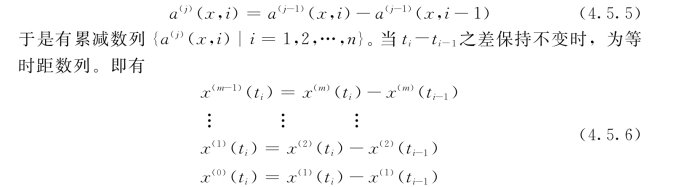
4.5.1.2　光滑离散函数

由于GM建模一般是针对离散数列而言的，因而要求它符合灰指数律，并可用光滑离散函数来描述。所谓光滑离散函数是与光滑函数相比较而言的，当离散函数与光滑函数的性质大致相近时，就可认为它是某一光滑函数的离散形式。

判断一个离散函数是否光滑的弱条件：设X（0）为非负离散函数

令

在所有的GM 模型中，作预测用的GM 模型一般为GM（n，1）模型。其中，在实际中应用得最多的是GM（1，1）模型。本节研究的是等时距序列GM（1，1）模型。

4.5.1.3　GM（1，1）模型的求解

设X（0）为原始非负序列

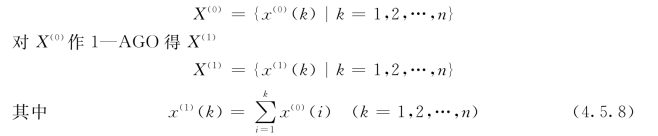
检验X（0）是否满足准光滑性条件，即

如果存在m（m＝1，2，…，n），当k＞m 时，ρ（k）＜0.5，那么满足准光滑条件。

检验X（1）是否满足准指数规律，即

如果存在m（m＝1，2，…，n），当k＞m 时，σ（k）［1，1.5］，δ＝0.5，那么满足准指数规律。

(www.daowen.com)

GM（1，1）模型的基本形式为如下灰色微分方程

用最小二乘法求解参数a、b，得

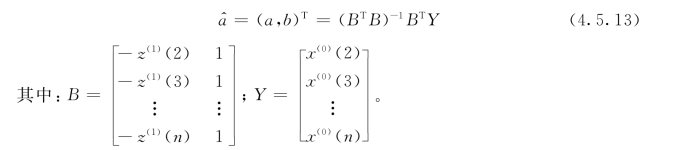
GM（1，1）模型的白化方程为

式（4.5.14）的解（也称为时间响应函数）为

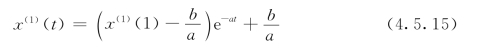
则式（4.5.12）的时间响应函数序列为

4.5.1.4　GM（1，1）模型的特性及适用范围

研究表明，GM（1，1）模型的有效性与其发展系数－a 的取值区间有关。一般地，当｜a｜＜2 时，GM（1，1）模型有意义。但随着a 的不同取值，预测效果也不同。对于－2＜a＜0，即发展系数0＜－a＜2 的情形，刘思峰等（2000）对－a 分别取不同的值进行了模拟分析，得到了以下结论。

1）当－a≤0.3 时，GM（1，1）模型可用于中长期预测。

2）当0.3＜－a≤0.5 时，GM（1，1）模型可用于短期预测，中长期预测慎用。

3）当0.5＜－a≤0.8时，用GM（1，1）模型作短期预测应十分谨慎。

4）当0.8＜－a≤1 时，应采用残差修正GM（1，1）模型。

5）当－a＞1 时，不宜采用GM（1，1）模型。

可见，依据GM（1，1）模型进行预测，必需一定的检验手段。为提高预测精度，必要时应对残差作进一步处理，也就是需要进行原始数据序列的残差辨识；而当残差值达到规定时，才能进行预测。GM（1，1）模型的预测精度通常用后验差检验方法进行检验。

令S1 为原始数据列的均方差，S2 为残差序列的均方差，其表达式分别为：

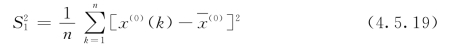
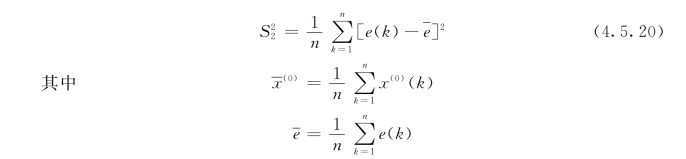
然后，计算后验差比值C 以及小误差概率p，其表达式分别为：

一般地，可按照p 和C 值将模型的精度分为四级（傅立，1992），见表4.5.1。显然，只有当p、C 值均在允许范围之内，方可将所建模型用于预测；否则需进行残差修正以保证预测结果的可靠性。

表4.5.1　GM（1，1）模型精度检验的经验指标