小波网络是基于小波分析而构造的一种前馈网络，即用非线性的小波基代替常用的非线性Sigmoid函数，通过将所选取的小波基进行线性叠加来实现。它结合了小波变换良好的时频局部化性质和传统神经网络的自学习功能，因而具有较强的逼近和容错能力。与传统的神经网络系统相比，它具有以下特点：首先，小波基元与整个网络结构的确定有可靠的理论根据，可以避免以往神经网络结构设计的盲目性；其次，通过小波分析研究神经网络，隐节点个数可以自适应确定，解决了传统神经网络隐层节点个数难以确定的问题；最后，还具有比一般网络更强的函数学习和推广能力。

在探讨小波网络理论时，小波和小波分解是两个重要的概念。

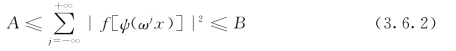
则ψ（x）为二进制小波。

关于小波变换，可利用小波函数进行定义。函数f（x）的连续小波可变换为

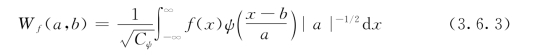
其逆变换为

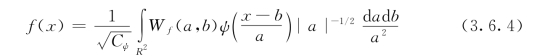
可见小波变换是通过小波的伸缩和平移而得到的。另外，小波变换还具有如下性质。(www.daowen.com)

（1）叠加性：设f（x），g（x）∈L2（R），k1k2为任意实数，则

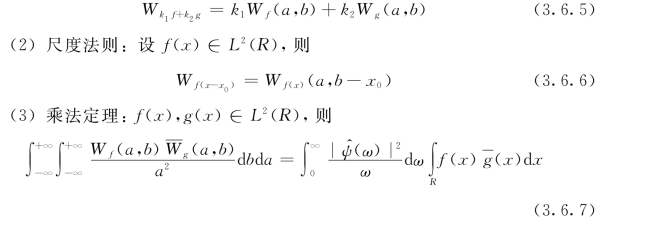
（4）能量关系：描述了小波变换与原函数之间的能量关系，取f（x）＝g（x），可得出与傅立叶变换中的Parseval等式相类似的表达式

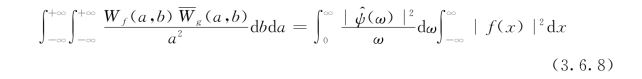
（5）反演公式：f（x）∈L2（R），则

式中：g（x）∈R为输出向量，x∈Rn为输入向量，bij、aij分别为隐含层小波基的平移因子和伸缩因子，ωj 为隐含层到输出层的权值，ψ（·）为小波基函数。有关模型的结构见图3.6.1。

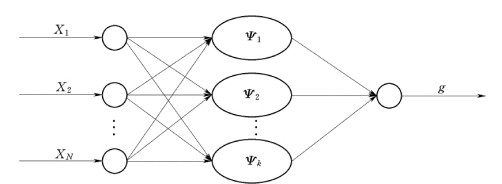
图3.6.1　小波网络模型结构图

图3.6.1 中输入层有N 个节点，隐含层有K 个节点，输出层有1 个节点。给定m组输入、输出样本，xn（n＝1，…，N）为网络输入，g 为网络输出，ψk（k＝1，…，K）则为小波基函数。使用小波基设计处理网络，可使训练问题大大简化。