根据上述分析可知，库水位、降雨这两个环境量对大坝基础渗流量的影响具有一定的时间上的滞后。如何刻画这种滞后效应，一般可根据渗流量过程线与库水位过程线进行图形比较确定，即两个过程线从稳定状态发生变化的时间之差或两过程线出现峰谷的时间之差作为滞后时间。本节针对这一现象，在常规分析方法的基础上，考虑水位（或降雨）的滞后影响，建立基于这种滞后效应的渗流统计模型（张乾飞等，2001）。

首先，探讨库水位的滞后效应。应该说，随时间而连续变化的坝基渗流量是库水位（包括降雨、温度和时效）等环境量动态变化作用下的瞬时效应量，而库水位H 是随时间t 的函数。显然，渗流量Q（t）是库水位H 的伴随函数，同时又滞后于H 的变化，即

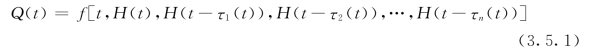
式中：τ为滞后时间；τk（t）≥0，k＝1，2，…，n；H（t），H（t－τk（t））为对应时刻的库水位。

可见，Q（t）是带有时滞变元的函数，它反映了库水位的峰谷变化与渗流量滞后变化之间的相关关系，表明t 时刻渗流量Q（t）是此前库水位连续变化影响的瞬态结果。

由于渗流量要滞后上游水位一定的时间，采用常规的统计模型一般选用前期水位的平均值作为考虑滞后效应的水位影响因子，如式（3.4.2）所示。然而，在基于回归分析建立模型时，有时前1 个月及其以上的平均水位也有可能被选入，最后难以解释。若设库水位对渗流的影响在第i 天产生最大效应，显然经历了在这之前逐渐增大、之后逐渐减小的过程，而不应该是平均的过程。

设某渗流测点测值受观测日前m 天水位hi（i＝1，2，…，m）的影响，hd为某等效水位，在其作用下该测点在同一观测日有相同测值，则hd可由下式表示

由于库水位和渗流量是随时间变化的连续函数，因此，等效水位也是时间t 的连续函数。设相应的权分布函数为w（t），且t∈Ω，Ω为影响渗流测值的前期水位时间域。由渗流理论可知，设任意t0∈Ω，对于任意给定的正数ε，显然存在着正数δ，使得对于适合不等式｜t－t0｜＜δ的一切t，所对应的函数值w（t）都满足不等式

即w（t）也为时间的连续函数。

设水位滞后天数为x1，影响天数为x2，根据统计分析，w（t）一般呈正态分布，则其滞后影响函数为

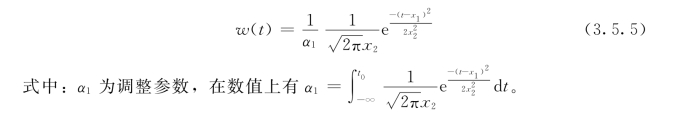
对某一测点而言，在一定时段内，可认为滞后天数x1和影响天数x2为常数，因此在固定观测日（t＝t0），α1为常数。则恒有

显然，w（t）≥0。因此，w（t）可作为前期水位对等效水位影响权的分布密度函数。

固定测点在t＝t0时刻测值的等效水位为hd（t），前期水位对其影响的权函数为w（t）≥0。则

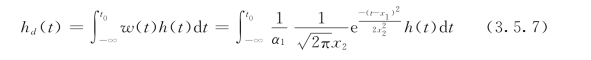(www.daowen.com)

这样，可得到渗流量的库水位分量Qh表达式

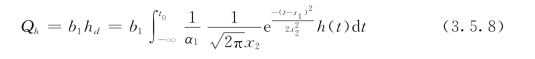
式中：b1为水位分量的回归系数；x1为待定的水位滞后天数；x2为待定的水位影响天数；h（t）为t 时刻的水位；hd为等效水位。

对于式（3.5.8）中的x1、x2，可通过优化计算求得。经优化可找到实际的滞后天数和影响天数。通常，每天都有水位测值，因此可把连续型积分改成离散型积分。根据统计学理论，积分区间只需取x2的2～3 倍即可满足要求。

然后，探讨降雨对坝基渗流的影响滞后效应。在时间上，降雨与渗流之间也有一个滞后过程，其作用机理与上述水位分量相似。因此，降雨分量也采用与式（3.5.8）相似的滞后模式。即

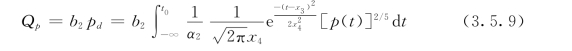
式中：Qp为降雨分量；b2为降雨分量的回归系数；x3为待定的降雨滞后天数；x4为待定的降雨影响天数；p（t）为t 时刻的降雨量；pd为等效降雨量。

对于该式中的x3和x4通过计算求得，并通过化连续积分为离散型积分来实现。

在考虑了库水位、降雨对坝基渗流的具体影响以及温度和时效产生的相应影响之后，可建立如下基于滞后效应的渗流统计模型

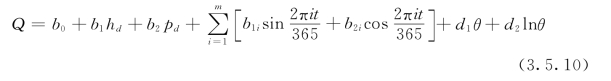
利用最优化原理可求得式（3.5.10）中的系数bj（j＝0～2）、b1i、b2i（i＝1～m）、ds（s＝1～2）。其求解步骤，首先令

若M 有最小值，则必有

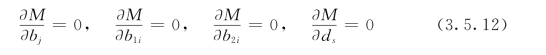
之后，利用式（3.5.8）和式（3.5.9），根据实测资料，可求得一组对应库水位及降雨量的滞后天数和影响天数条件下的回归系数bj（j＝0～2）、b1i、b2i（i＝1～m）、ds（s＝1～2）以及复相关系数R、剩余均方差S 等。并以复相关系数为衡量标准，通过对水位分量及降雨分量的滞后天数和影响天数的假定和修正，逐次迭代逼近，最后找到一组使复相关系数最大的滞后天数及影响天数，同时也得到一组回归系数及其他参数值。

上述基于滞后效应的渗流统计模型，其数值计算流程如图3.5.1 所示。