1.1.6　练习

1.南京，北京∈中国城市.

2.有限集：（2），（3）；无限集：（1），（4）.

3.（1）{x|0≤x＜4并且x∈Z+}={0，1，2，3}

（2）{x|x=5k并且k∈Z}=

（3）{x|x=3k并且k∈Z+}={3，32，33，…，3k，…}

4.（1）A1={2，3，4，5，6，7，8，9}

（2）A2={2，5}

（3）A3={＜0，-1＞，＜0，0＞，＜0，1＞，＜1，-1＞，＜1，0＞，＜1，1＞，＜2，-1＞，＜2，0＞，＜2，1＞，＜3，-1＞，＜3，0＞，＜3，1＞}

5.正确的有：

∅⊆∅，∅⊆{∅}，∅∈{∅}，{a，b}⊆{a，b，{a，b}}，{a，b}∈{a，b，{a，b}}，{a，b}⊆{a，b，{{a，b}}}.

6.∅∈{∅}，{∅}∈{{∅}}，∅∉{{∅}}.

7.（2）取A={∅}，B=C={{∅}}，则A∈B并且B=C，但A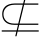C.

（3）A={∅}，B={∅，{∅}}并且C={{∅，{∅}}}，则A⊆B并且B∈C，但A∉C.

（4）同上.

8.A=B=C=D=F，E=G.

9.（1）℘（{1，2，3}）={∅，{1}，{2}，{3}，{1，2}，{1，3}，{2，3}，{1，2，3}}.

（2）℘（{1，{2，3}}）={∅，{1}，{{2，3}}，{1，{2，3}}}.

（3）℘（{{∅，2}，{2}}）={∅，{{∅，2}}，{{2}}，{{∅，2}，{2}}}.

10.（1）℘（∅）={∅}.

（2）℘（℘（∅））={∅，{∅}}.

（3）℘（℘（℘（∅）））={∅，{∅}，{{∅}}，{∅，{∅}}}.

11.略.

12.略.

1.2.6　练习

1.（1）A∪B={a，b，c，e}；

（2）A∩B={a，c}；

（3）A∪B∪C={a，b，c，d，e，f}；

（4）A∩B∩C=∅；

（5）A-B={b}；

（6）B-C={a，c，e}.

2.A′=B，B′=A，（A∪B）′=∅，（A∩B）′=E.

3.（1）A∩B={x|4＜x＜5并且x∈R}.

（2）A∪B={x|3＜x并且x∈R}.

（3）A-B={x|3＜x≤4并且x∈R}.

4.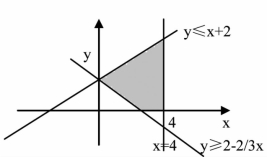图中化线部分.

5.（1）A′={4，5，6}； （2）B′={1，3，5}； （3）A′∪B′={1，3，4，5，6}；

（4）A′∩B′={5}.

6.a=1，b=2.

7.（1）{3，{3}，4，{4}}；（2）{∅}；（3）{∅，{∅}}.

8.（1）{∅，{{∅}}，{{{∅}}}，{{∅}，{{∅}}}}.

（2）{∅，{∅}}.

（3）∅.

（4）{∅，{∅}，{{∅}}，{∅，{∅}}}.

（5）∅.

9.（1）{1，2，3}；（2）∅.（3）∅.（4）∅.

10.（1）{a，b}.（2）a.（3）∅.

11.略.

12.（1）A∩B∩C.（2）（A∪B）∪C.（3）C∪（A∩B）.

13.4={∅，{∅}，{∅，{∅}}，{∅，{∅}，{∅，{∅}}}.

14.略.

15.0，0，1，0，2，0，{0，1，2，{1}}.

16.2.

17.2.

18.{{1}，{2}，{0，2}，{1，2}，3}.

19.略.

1.3.6　练习

1.（1）{＜＜0，1＞，1＞，＜＜0，1＞，2＞，＜＜1，1＞，1＞，＜＜1，1＞，2＞}，

（2）{＜＜0，0＞，1＞，＜＜0，0＞，2＞，＜＜0，1＞，1＞，＜＜0，1＞，2＞＞，＜＜1，0＞，1＞，＜＜1，0＞，2＞，＜＜1，1＞，1＞，＜＜1，1＞，2＞}，

（3）{＜＜1，0＞，＜1，0＞＞，＜＜1，0＞，＜1，1＞＞，＜＜1，0＞，＜2，0＞＞，＜＜1，0＞，＜2，1＞＞，

＜＜1，0＞，＜2，1＞＞，＜＜1，1＞，＜1，0＞＞，＜＜1，1＞，＜1，1＞＞，＜＜1，1＞，＜1，0＞＞，

＜＜2，0＞，＜1，0＞＞，＜＜2，0＞，＜1，1＞＞，＜＜2，0＞，＜2，0＞＞，＜＜2，0＞，＜2，1＞＞，

＜＜2，1＞，＜1，0＞＞，＜＜2，1＞，＜1，1＞＞，＜＜2，1＞，＜2，0＞＞，＜＜2，1＞，＜2，1＞＞}.

2.{＜∅，1＞，＜∅，2＞，＜{1}，1＞，＜{1}，2＞，＜{2}，1＞，＜{2}，2＞，＜{1，2}，1＞，＜{1，2}，2＞}.

3.略.

4.略.

5.A∪B={＜1，2＞，＜2，4＞，＜3，3＞，＜1，3＞，＜4，2＞}，A∩B={＜2，4＞}，A-B={＜1，2＞，＜3，3＞}，dom（A）={1，2，3}，dom（B）={1，2，4}，dom（A∪B）={1，2，3，4}，ran（A）={2，3，4}，ran（B）={2，3，4}，ran（A∩B）={4}，fld（A）={1，2，3，4，}=fld（B）.

6.R◦R={＜0，1＞，＜0，3＞，＜0，3＞，＜1，3＞，＜0，1＞}，R∴{1}={＜1，2＞，＜1，3＞}，R[{1}]={2，3}，R-1[{1}]={0}.

7.略.

8.略.

9.R={＜1，9＞，＜9，1＞，＜2，8＞，＜8，2＞，＜3，7＞，＜7，3＞，＜4，6＞，＜6，4＞，＜5，5＞}具有对称性.

10.R1◦R2={＜a，d＞，＜a，c＞，＜b，d＞}，R2◦R1={＜c，d＞}，

R1◦R1={＜a，a＞，＜a，b＞，＜a，d＞}，R2◦R2={＜b，b＞，＜a，c＞，＜c，c＞，＜c，d＞}.

11.R1=∅，R2={＜a，s＞}，R3={＜b，s＞}，R4={＜c，s＞}，R5={＜a，s＞，＜b，s＞}，R6={＜a，s＞，＜c，s＞}，R7={＜c，s＞，＜b，s＞}，R8={＜a，s＞，＜b，s＞，＜c，s＞}.

12.∅，{＜∅，∅＞}.

13.2n×n.

14.略.

15.略.

16.略.

17.略.

18.3={0，1，2}，3×3={＜0，0＞，＜0，1＞，＜0，2＞，＜1，0＞，＜1，1＞，＜1，2＞，＜2，0＞，＜

2，1＞，＜2，2＞}

R1={＜0，0＞，＜1，1＞，＜2，2＞}

R2={＜0，0＞，＜1，1＞，＜2，2＞，＜0，1＞，＜1，0＞}

R3={＜0，0＞，＜1，1＞，＜2，2＞，＜0，2＞，＜2，0＞}

R4={＜0，0＞，＜1，1＞，＜2，2＞，＜2，1＞，＜1，2＞}

R5={＜0，0＞，＜1，1＞，＜2，2＞，＜0，1＞，＜1，0＞，＜0，2＞，＜2，0＞}

R6={＜0，0＞，＜1，1＞，＜2，2＞，＜0，1＞，＜1，0＞，＜1，2＞，＜2，1＞}

R7={＜0，0＞，＜1，1＞，＜2，2＞，＜2，1＞，＜1，2＞，＜0，2＞，＜2，0＞}

R8={＜0，0＞，＜0，1＞，＜0，2＞，＜1，0＞，＜1，1＞，＜1，2＞，＜2，0＞，＜2，1＞，＜2，2＞}

以上R1到R8均是3上的等价关系.

19.-21.略.

22.方法类似于第18题.

23.-26.略.

27.3={0，1，2}，3×3={＜0，0＞，＜0，1＞，＜0，2＞，＜1，0＞，＜1，1＞，＜1，2＞，＜2，0＞，＜2，1＞，＜2，2＞}

R1={＜0，0＞，＜1，1＞，＜2，2＞}

28.∅可以是一个等价关系，也是一个序.

29.-30.略.

1.4.4　练习

1.（2）.

2.（1）dom（R1）={1，2，3，4}，ran（R1）={＜2，3＞，＜3，4＞，＜1，4＞}并且R1是一个函数.

（2）dom（R2）={1，2，3}，ran（R2）={＜2，3＞，＜3，4＞，＜3，2＞}并且R2是一个函数.

（3）dom（R3）={1，2}，ran（R3）={＜2，3＞，＜3，4＞，＜2，4＞}.

（4）dom（R4）={1，2，3}，ran（R4）={＜2，3＞}并且R4是一个函数.

3.略.

4.（1）I={＜∅，∅＞}.（2）∅.

（3）F1={＜＜0，0＞，0＞，＜＜0，1＞，1＞，＜＜0，2＞，2＞，＜＜1，0＞，3＞，＜＜1，1＞，4＞，＜＜1，2＞，5＞}是2×3到6的双射；F2={＜0，＜0，0＞＞，＜1，＜0，1＞＞，＜2，＜0，2＞＞，＜3，＜1，0＞＞，＜4，＜1，1＞＞，＜5，＜1，2＞＞}是6到2×3的双射.

5.（1）23={f|f：3→2}={f1，f2，f3，f4，f5，f6，f7，f8}，其中f1，f2，f3，f4，f5，f6，f7，f8满足下面的表：

（2）32={f|f：2→3}={f1，f2，f3，f4，f5，f6，f7，f8，f9}，其中f1，f2，f3，f4，f5，f6，f7，f8，f9满足下面的表：

（3）20={f|f：0→2}={∅}

（4）02={f|f：2→0}=不存在

（5）00={f|f：0→0}={∅}

（6）10={f|f：0→1}={∅}

（7）11={f|f：1→1}={f}，其中f={＜0，0＞}.

（8）01={f|f：1→0}=不存在

（9）21={f|f：1→2}={f1，f2}，其中f1={＜0，0＞}，f2={＜0，1＞}.

（10）12={f|f：2→1}={f}，其中f={＜0，0＞，＜1，0＞}.

6.（1）单射.

7.（1）f={＜1，a＞，＜2，b＞＜3，c＞}.

（2）A={A1，A2，A3，A4，A5，A6，A7，A8}，其中：A1，A2，A3，A4，A5，A6，A7，A8分别是：

∅，{a}，{b}，{c}，{a，b}，{a，c}，{b，c}，{a，b，c}.

B={f1，f2，f3，f4，f5，f6，f7，f8}，其中f1，f2，f3，f4，f5，f6，f7，

f8满足下面的表：

令g：A→B满足：g（Ai）=Bi，i=1，2，3，4，5，6，7，8.

8.略.

9.g◦f（x）=2x+4，f◦g（x）=2x+7，f◦f（x）=2x+6，g◦g（x）=4x+3，f◦h（x）=（x+3）/2，h◦g（x）=x+1，h◦f（x）=x/2+3，f◦h◦g（x）=x+4.

10.f◦f（n）=n+2，f◦g（n）=2n+2，g◦f（n）=2n+1，f◦h◦g（n）=0.

11.-13.略.

2.2.4　练习

1.（1），（5），（7），（8），（11），（14），（15），（16），（17），（18），（20），（21），（22），（23），（25），其余的不是.

2.（1）合取形式的复合命题

（2）合取形式的复合命题

（3）蕴涵形式的复合命题

（4）析取形式的复合命题

（5）否定形式的复合命题

（6）析取形式的复合命题

（7）蕴涵形式的复合命题

（8）简单命题

（9）蕴涵形式的复合命题

（10）蕴涵形式的复合命题

3.解：令p：这个男孩知道答案

q：那个女孩知道答案

那么，复合命题：

男孩知道答案或者那个女孩知道答案

所对应的真值形式为：p∨q.它所对应的真值表如下：

因此，有如上的真值表可知：

（1）假并且q为真时，合命题p∨q取真值；

（2）真并且q为假时，合命题p∨q取真值.

4.答：（1）当p和q不同时p*q为真，即：p真q假或者p假q真时，p*q均为真；

（2）当p和q的取值确定后，p*q和p∧q的取值结果恰好相反。即：p*q真时p∧q反而为假，p*q假时p∧q反而为真.因此，

p*q=df﹁（p∧q）或者p*q=df﹁p∨﹁q.

5.答：图（1）对应着联结词∧，图（2）对应着联结词∨.如果p是闭的，q是开的，图

（1）中的灯不亮，图（2）中的灯会亮.在这种情况下，图（1）中的灯对应∧的真值表的第二行，图（2）中的灯对应∨的真值表的第二行.

6.略.

2.2.7　练习

1.（1）人不犯我，我不犯人；人若犯我，我必犯人.

解：令p：人犯我

q：我犯人

该命题可以形式表示为：（﹁p→﹁q）∧（p→q）.

（2）他将在明天或者后天去北京或天津.

解：令p：他明天去北京

q：他明天去天津

r：他后天去北京

s：他后天去天津

该命题可表示为：p∨q∨r∨s.

（3）除非知道了癌症的病因并且找到了治疗癌症的新药，否则癌症是不能治愈的.

解：令p：知道了癌症的病因

q：找到了治疗癌症的新药

r：治愈癌症

该命题可表示为：﹁（p∧q）→﹁r.

（4）我没有看见张三和李四.

解：令p：我看见张三

q：我看见李四

该命题可表示为：﹁（p∧q）.

（5）并非花都是红的.

解：令p：花是红的

该命题可表示为：﹁p

（6）今天不刮风也不下雨.

解：令p：今天刮风

q：今天下雨

该命题可表示为：﹁p∧﹁q.

（7）如果国会拒绝制定新的法令，那么罢工不会结束，除非它持续半年以上并且商号老板签约.

解：令p：国会制定新的法令

q：罢工结束

r：罢工持续半年以上

s：和商号老板签了约

该命题可表示为：﹁p→（﹁q∨（r∧s））.

2.答：如果命题p前﹁的个数为奇数，则此命题的真值与命题p的真值一致；否则如果在命题p前﹁的个数为偶数，则此命题的真值与命题p的真值恰好相反.

3.（1）q↔（（（﹁r）→（s∧q∧（（﹁r）∨p）））↔（q→（﹁r）））.

（2）（﹁﹁﹁q）↔（r↔（（（p∧r∧q∧（﹁﹁s））→（q→r））↔（﹁p）））.

4.（1）（（p∧q）→﹁r）↔（s∨t）.

（2）（（p∨q）∧r）→（﹁（s↔t））.(www.daowen.com)

5.（1）p∨q与﹁p→q的共享真值表如下：

（2）p→q与﹁p∨q的共享真值表如下：

（3）p↔q与（p→q）∧（q→p）的共享真值表如下：

（4）q→p与﹁p→﹁q的共享真值表如下：

6.（1）（（p→q）→r）→s

（2）（p↔q）↔p↔q↔p

（3）（p→q→r）→p∧q→q∨r

令α：（p→q→r）→p∧q→q∨r

（4）﹁（﹁p∧q→﹁（p↔r）∨q）

令α：﹁p∧q→﹁（p↔r）∨q

7.（1）真，（2）假，（3）假，（4）真，（5）假，（6）假.

8.f1（p，q）=p∨﹁p；f2（p，q）=p∨q；f3（p，q）=q→p；f4（p，q）=（p∧q）∨（p∧﹁q）；

F5（p，q）=p→q；f6（p，q）=（p∧q）∨（﹁p∧q）；f7（p，q）=p↔q；f8（p，q）=p∧q；

F9（p，q）=﹁（p∧q）；f10（p，q）=﹁（p↔q）；f11（p，q）=（p∧﹁q）∨（﹁p∧﹁q）；f12（p，q）=﹁（p→q）；

f13（p，q）=（﹁p∧q）∨（﹁p∧﹁q）；f14（p，q）=﹁（q→p）；f15（p，q）=﹁p∧﹁q；f16（p，q）=p∧﹁p.

9.（1）Hpqr的真值表如下：

（2）用﹁，∨，∧表示的Hpqr为：（﹁p∨q∨r）∧（p∨﹁q∨r）∧（p∨q∨﹁r）.

10.（1）Δpqr的真值表如下：

（2）用﹁，∨，∧表示的Δpqr为：（﹁p∨﹁q∨﹁r）∧（﹁p∨﹁q∨r）∧（﹁p∨q∨﹁r）∧（p∨﹁q∨﹁r）.

11.（p∨q）=df（（p→q）→q）.

12.（1）f10（p，q）=df（﹁（﹁p∨q）∨﹁（﹁q∨p））.

（2）f10（p，q）=df（﹁（﹁（p∧﹁q）∧﹁（q∧﹁p））.

（3）f10（p，q）=df（（p→q）→﹁（q→p））.

（4）f10（p，q）=df﹁（p↔q）.

13.﹁p=df（p|p）；（p→q）=df p|（p|q）.

14.﹁p=df（p↓p）；（p∧q）=df（p↓p）↓（q↓q）.

15.（1）﹁p=df（p↔·p）↔p；（p∨q）=df（p↔q）↔（p∧q）；（p→q）=df p↔（p∧q）.

（2）﹁p=df（p↔·p）↔p；（p∧q）=df（p↔q）↔（p∨q）；（p→q）=dfq↔（p∨q）.

（3）不能.

16.-18.略.

19.（1）可满足式；（2）重言式；（3）矛盾式；（4）可满足式；

（5）重言式；（6）重言式；（7）可满足式；（8）矛盾式.

20.略.

21.（1）蕴涵；（2）不蕴涵；（3）蕴涵；（4）蕴涵.

22.（1）﹁（p∧q∧﹁r）；（2）﹁（﹁p∨﹁q∨﹁r）∧﹁（p∨q∨r）；

（3）（p∧q∧﹁r）∨（p∧﹁q∧r）∨（﹁p∧q∧r）∨（﹁p∧﹁q∧﹁r）；

（4）p∧q∧﹁r.

23.（1）﹁p∨﹁q∨r；（2）﹁（﹁（﹁p∨﹁q∨﹁r）∨﹁（p∨q∨r））；

（3）﹁（﹁p∨﹁q∨r）∨﹁（﹁p∨q∨﹁r）∨﹁（p∨﹁q∨﹁r）∨﹁（p∨q∨r）；

（4）﹁（﹁p∨﹁q∨r）.

24.（1）是；（2）是；（3）是；（4）是；（5）不是；（6）是.

25.（1）是；（2）是；（3）是；（4）不是；（5）是；（6）不是；（7）是；（8）不是.

2.3.5　练习

1.（1）（p∨﹁p∨q∨r）∧（p∨﹁p∨q∨r）∧（﹁p∨q∨﹁q∨r）∧（﹁p∨﹁q∨r∨﹁r），是重言式.

（2）（﹁p∨q∨﹁p）∧（﹁p∨q∨﹁q）∧（p∨q∨p）∧（p∨q∨﹁q），不是重言式.

2.（1）﹁p∨（（p∧﹁p）∨（p∧q）），不是不可满足式.

（2）（p∧﹁q）∨p∨r，不是不可满足式.

3.（1）析取范式；（2）析取范式；（3）既不是析取范式也不是合取范式；

（4）既不是析取范式也不是合取范式；（5）既不是析取范式也不是合取范式；

（6）是合取范式；（7）优析取范式；（8）优合取范式；（9）合取范式.

4.（1）它们有相同的优析取范式：（p∧q∧r）∨（p∧q∧﹁r）∨（﹁p∧q∧r），所以它们表达同一真值函项.

（2）它们没有相同的优析取范式，所以它们不表达同一真值函项.

5.（1）（p∧﹁q∧r）∨（p∧﹁q∧﹁r）∨（﹁p∧q∧r）∨（﹁p∧﹁q∧r）；

（2）（p∧q∧﹁r）∨（p∧﹁q∧r）∨（p∧﹁q∧﹁r）∨（﹁p∧q∧r）∨（﹁p∧q∧﹁r）∨（﹁p∧﹁q∧r）；

（3）（p∧q∧r）∨（p∧q∧﹁r）∨（p∧﹁q∧﹁r）∨（﹁p∧q∧r）∨（﹁p∧q∧﹁r）；

（4）（p∧q∧﹁r）∨（p∧﹁q∧r）∨（p∧﹁q∧﹁r）∨（﹁p∧q∧r）∨（﹁p∧q∧﹁r）∨（﹁p∧﹁q∧r）.

6.（1）（p∨q∨﹁r）∧（p∨﹁q∨r）∧（p∨﹁q∨﹁r）∧（﹁p∨q∨r）∧（﹁p∨q∨﹁r）∧（﹁p∨﹁q∨r）.

（2）（p∨q∨﹁r）∧（p∨﹁q∨r）∧（p∨﹁q∨﹁r）∧（﹁p∨﹁q∨r）∧（﹁p∨﹁q∨﹁r）.

（3）（p∨q∨﹁r）∧（p∨﹁q∨r）∧（p∨﹁q∨﹁r）∧（﹁p∨q∨r）∧（﹁p∨q∨﹁r）∧（﹁p∨﹁q∨r）.

（4）（p∨﹁q∨r）∧（p∨﹁q∨﹁r）∧（﹁p∨q∨r）∧（﹁p∨﹁q∨r）.

7.（1）的优合取范式为：（p∨q）∧（﹁p∨q）；优析取范式为：（p∧q）∨（﹁p∧q）.

（2）的优合取范式为：∅；优析取范式为：（p∧q）∨（p∧﹁q）∨（﹁p∧q）∨（﹁p∧﹁q）.

（3）的优合取范式为：（p∨q∨r）∧（p∨q∨﹁r）∧（p∨﹁q∨﹁r）；优析取范式为：（p∧q∧r）∨（p∧q∧﹁r）∨（p∧﹁q∧r）∨（p∧﹁q∧﹁r）∨（﹁p∧q∧﹁r）.

8.（1）的优析取范式为：

（p∧q∧r）∨（p∧q∧﹁r）∨（p∧﹁q∧r）∨（﹁p∧q∧r）∨（﹁p∧q∧﹁r）∨（﹁p∧﹁q∧r）∨（﹁p∧﹁q∧﹁r）.当（p，q，r）分别取值为：（真，真，真），（真，真，假），（真，假，真），（假，真，真），（假，假，真），（假，假，假）时，原式的值为真.

（2）的优析取范式为：（p∧q）∨（p∧﹁q）∨（﹁p∧q）∨（﹁p∧﹁q）.

当（p，q）分别取值为：（真，真），（真，假），（假，真），（假，假）时，原式的值为真.

9.（1）的优析取范式为：（p∧q）∨（p∧﹁q），当（p，q）分别取值为：（真，真），（真，假）时，原式的值为真.

（2）的优析取范式为：（p∧﹁q）∨（﹁p∧q）∨（﹁p∧﹁q）.

当（p，q）分别取值为：（真，假），（假，真），（假，假）时，原式的值为真.

10.（1）的一个合取范式为：

（p∨﹁p∨p）∧（p∨﹁p∨﹁q）∧（﹁p∨p∨q）∧（﹁p∨p），所以原式是一个重言式.

（2）的一个合取范式为：

（p∨﹁p∨q∨r）∧（﹁q∨﹁p∨q∨r）∧（﹁r∨﹁p∨q∨r）∧（﹁p∨q∨r∨p）∧（﹁p∨q∨r∨﹁q）∧（﹁p∨q∨r∨﹁r），

所以原式是一个重言式.

（3）的一个合取范式为：

（p∨﹁p∨q∨r）∧（﹁q∨﹁p∨q∨r）∧（﹁r∨﹁p∨q∨r）∧（﹁p∨q∨p）∧（﹁p∨q∨﹁q）∧（﹁p∨﹁q∨﹁p∨q），

所以原式是一个重言式.

（4）的一个合取范式为：

（﹁p∨q∨﹁p∨r∨p）∧（﹁p∨q∨﹁p∨r∨﹁q）∧（﹁p∨q∨﹁p∨r∨﹁r）∧（﹁p∨q∨r∨p）∧（﹁p∨q∨r∨﹁q）∧（﹁p∨q∨r∨p）∧（﹁p∨q∨r∨﹁r），

所以原式是一个重言式.

11.

由上面的真值表可知：是a.

12.q∧（p∨﹁q）的一个合取范式为：q∧（p∨﹁q）；析取范式为：（q∧p）∨（q∧﹁q）；优合取范式为：（p∨q）∧（p∨﹁q）∧（﹁p∨q）；优析取范式为：p∧q；当（p，q）取（真，真）时，原式取真值，其余情况下，原式取假值.

13.（1）（p∨q）∧（p∨﹁q）∧（﹁p∨q）；（2）p∨q；（3）﹁p∨q；（4）（p∨﹁q）∧（﹁p∨q）.

14.（1）的准否定式为：﹁p∨（﹁q∧（p∨﹁r）），对偶式为：p∨（q∧（﹁p∨r）；

（2）的准否定式为：（p∧﹁q）∧（p∧q）），对偶式为：（﹁p∧q）∨（﹁p∧﹁q）；

（3）的准否定式为：（p∧q）∧（﹁p∨q），对偶式为：（﹁p∧﹁q）∧（﹁p∨﹁q）；

（4）的准否定式为：（﹁p∧q）∨（﹁p∧﹁q）∨（p∧q），对偶式为：（p∧﹁q）∨（p∧q）∨（﹁p∧﹁q）.

3.1.5　练习

略.

3.2.4　练习

1.（1），（7）不是；（2），（3），（4），（5），（6）是.

2.（1），（2），（3），（4）是，其中（1），（4）是重言式，（3）为可满足式.

3.3.3　练习

略.

3.4.2　练习

略.

3.6.3　练习

1.0；2.1；1；4.1；5.0；6.0.

2.成立.

3.-4.略.

5.正确.

4.1.2　练习

略.

5.1.5　练习

1.∀x（F（x）→P（x）），

其中：∀x：凡x，F（x）：x是一个事物，P（x）：x是发展变化的.

2.∀x（F（x）→∃y（P（y）∧x=y）），

其中：∀x：凡x，∃y：存在一个y，F（x）：x是一个有理数，P（y）：y是一个分数.

3.∀x∀y（F（x）∧F（y）→x≥y∨y≥x），

其中：∀x：凡x，F（x）：x是一个实数.

4.∃x（F（x）∧P（x）），

其中：∃x：有一个x，F（x）：x是一个事物，P（x）：x有新陈代谢.

5.∃x（F（x）∧P（x）），

其中：∃x：有一个x，F（x）：x是一个自然数，P（x）：x是一个素数.

6.∀x（F（x）→∀y（P（y）→R（x，y））），

其中：∀x：所有的x，F（x）：x是一个参观者，P（y）：y是一件展品，R（x，y）：x欣赏y.

7.∀x（F（x）→∃y（P（y）∧R（x，y））），

其中：∀x：所有的x，F（x）：x是一个参观者，P（y）：y是一件展品，R（x，y）：x欣赏y.

8.∃x（F（x）∧∀y（P（y）→R（x，y））），

其中：∀x：所有的x，F（x）表示：x是一个参观者，P（y）表示：y是一件展品，R（x，y）：x欣赏y.

9.∃x（F（x）∧∃y（P（y）∧R（x，y））），

其中：∀x：所有的x，F（x）：x是一个参观者，P（y）：y是一件展品，R（x，y）：x欣赏y.

10.∀x（F（x）→∀y（P（y）→R（x，y））），

其中：∀x：每一个x，F（x）：x是一个人，P（x）：x是一名教师，R（x，y）：x尊敬y.

11.﹁（∀x（F（x）→∀y（y∈x→R（y，c）））），

其中：∀x：每一个x，F（x）：x是一个班级，y∈x：y是x班的学生，c：这门课，R（y，c）：y喜欢c.

12.∃x（P（x）∧∀y（F（y）∧Q（y）→R（x，y））），

其中：P（x）：x是一个学生，F（有）：y是一名教师，Q（y）：棋下的好，R（x，y）：x喜欢y.

13.∀x（R（c，x）→H（c，x）），

其中：c：张三，R（c，x）：c是x的对手，H（c，x）：c打败了x.

14.∀x（R（c，x）→H（x，c））.

2.（1）令R（v1，v2）：v1∈v2，其中v1和v2是集合，因此，∃v1∀v2（﹁R（v1，v2））表示：存在没有元素的集合.

（2）令R（v1，v2）：v1∈v2，其中v1和v2是集合，因此，∀v1∃v2∀v3（R（v2，v3）↔∀v4（R（v3，v4）→R（v1，v4））表示v2=∩v1.

（3）令R（v1，v2）：v1∈v2，其中v1和v2是集合，因此，∀v1∃v2∀v3（R（v2，v3）↔∃v4（R（v3，v4）→R（v1，v4））表示v2=∪v1.

3.（1）（3）（5）（6）是一阶公式，其余不是.

4.以下各题中，划线部分表示量词的狭域.

（1）R（x，y）→R（y，x）∧∀y Q（y），

其中，x的两次出现都是自由的，y的前两次出现是自由的，后一次出现是约束的.

（2）∀x（P（x）→∃y（R（x，y）∧Q（y）））并且∀x（P（x）→∃y（R（x，y）∧Q（y））），

其中，x的三次出现都是约束的，y的三次出现是约束的.

（3）∃x（P（x）→Q（x））→（P（y）→Q（y）），

其中，x的三次出现都是约束的，y的两次出现是自由的.

（4）∀y（R（x，y）∧Q（y））∨∀x P（x），

其中，x的第一次出现是自由的，或两次出现是约束的，y的两次出现是约束的.

（5）∀x∃y R（x，y）→∃y R（z，y），∀x∃y R（x，y）→∃y R（z，y）

其中，x的两次出现是约束的，y的前两次出现是约束的，y的后两次出现也是约束的，z的出现是自由的.

（6）∃x P（x）∨∃x R（x，y）→P（y）∨∀x R（x，y），

其中，x的前两次出现是约束的，第三、四次出现也是约束的，第五、六次出现是约束的，y的三次出现都是自由的.

（7）∃x∀y R（y，x，z）→∃zR（y，x，z），∃x∀y R（y，x，z）→∃zR（y，x，z），

其中，x的前两次出现是约束的，最后一次出现是自由的；y的前两次出现是约束的，最后一次出现是自由的；z的第一次出现是自由的，后两次出现是约束的.

（8）∀x∃y R（x，y）∧∃z Q（z，y，x），∀x∃y R（x，y）∧∃zQ（z，y，x），

其中，x的前两次出现是约束的，x最后一次出现是自由的；y的前两次出现是约束的，最后一次出现是自由的；z的两次出现都是约束的.

5.（1）sub（R（x，y）→R（y，x）∧∀y Q（y））

={R（x，y），R（y，x），∀y Q（y），R（y，x）∧∀y Q（y），R（x，y）→R（y，x）∧∀y Q（y）}

free（R（x，y）→R（y，x）∧∀y Q（y））={x，y}

（2）sub（∀x（P（x）→∃y（R（x，y）∧Q（y））））

={P（x），R（x，y），Q（y），R（x，y）∧Q（y），∃y（R（x，y）∧Q（y）），P（x）→∃y（R（x，y）∧Q（y））），

∀x（P（x）→∃y（R（x，y）∧Q（y）））}

free（∀x（P（x）→∃y（R（x，y）∧Q（y））））=∅

（3）sub（∃x（P（x）→Q（x））→（P（y）→Q（y）））

={P（x），Q（x），P（y），Q（y），P（x）→Q（x），P（y）→Q（y），∃x（P（x）→Q（x）），

∃x（P（x）→Q（x））→（P（y）→Q（y））}

free（∃x（P（x）→Q（x））→（P（y）→Q（y）））={y}

（4）sub（∀y（R（x，y）∧Q（y））∨∀x P（x））

={R（x，y），Q（y），R（x，y）∧Q（y），∀y（R（x，y）∧Q（y）），P（x），∀x P（x），∀y（R（x，y）∧Q（y））∨∀x P（x）}

free（∀y（R（x，y）∧Q（y））∨∀x P（x））={x}

（5）sub（∀x∃y R（x，y）→∃y R（z，y））

={R（x，y），∃y R（x，y），∀x∃y R（x，y），R（z，y），∃y R（z，y），∀x∃y R（x，y）→∃y R（z，y）}

free（∀x∃y R（x，y）→∃y R（z，y））={z}

（6）sub（∃x P（x）∨∃x R（x，y）→P（y）∨∀x R（x，y））

={P（x），∃x P（x），R（x，y），∃x R（x，y），∃x P（x）∨∃x R（x，y），P（y），R（x，y），∀x R（x，y），

P（y）∨∀x R（x，y），∃x P（x）∨∃x R（x，y）→P（y）∨∀x R（x，y）}

free（∃x P（x）∨∃x R（x，y）→P（y）∨∀x R（x，y））={y}

（7）sub（∃x∀y R（y，x，z）→∃zR（y，x，z））

={R（y，x，z），∀y R（y，x，z），∃x∀y R（y，x，z），∃z R（y，x，z），∃x∀y R（y，x，z）→∃zR（y，x，z）}

free（∃x∀y R（y，x，z）→∃z R（y，x，z））={x，y，z}

（8）sub（∀x∃y R（x，y）∧∃zQ（z，y，x））

={R（x，y），∃y R（x，y），∀x∃y R（x，y），Q（z，y，x），∃zQ（z，y，x），∀x∃y R（x，y）∧∃zQ（z，y，x）}

free（∀x∃y R（x，y）∧∃zQ（z，y，x））={x，y}

6.-7.略.

5.2.3　练习

1.-4.略.

5.4.2　练习

1.-2.略.

5.5.2　练习

1.-13.略.

5.6.3　练习

1.-5.略.