在数学理论中，离不开等号和运算符号.因此，在数学的形式化中，引进等词和运算符号也是相当自然的.然而，不用等词和运算符号，当然也能表达数学陈述.但是，在一般的情况下，都是比较麻烦的.本节将在第二至六章的基础上，建立带等词和运算符号的狭谓词逻辑.

要建立带等词和运算符号的狭谓词逻辑，只需要把第二至六章中有关的语法和语义概念做适当的改变.下面，我们将用“=”（等号）表示等词，用字母f，g，h等表示个体域上的运算符号.在叙述中，我们还将省略“带等词和运算符号的”修饰语.

定义6.1 一阶语言的字母表由下列符号组成：

（1）个体变项：v0，v1，v2，…和T，F；

（2）逻辑联结词：⇁，∨；

（3）量词：∀，∃；

（4）等词：=；

（5）技术性符号：，，（，）；

（6）对每个自然数n≥1，有一组（可以没有）n元关系符号；

（7）对每个自然数n≥1，有一组（可以没有）n元运算符号；

（8）有一组（可以没有）个体常项：c0，c1，c2，…

约定：用A表示上面（1）～（5）中所列举的全部符号.用S表示（6）～（8）中所列举的全部符号.A中的符号仍然被称为逻辑符号，S中的符号仍然被称为非逻辑符号.也就是说，等词“=”虽然是一个二元关系符号，但它是作为一个逻辑符号出现的.另外，A∩S=∅，并且AS=A∪S.

定义6.2 S项的归纳定义如下：

（1）个体变项和S中的个体常项统称S项；

（2）如果符号序列t0，t1，…，tn-1都是S项而且f是S中的一个n元关系符号，那么f（t0，t1，…，tn-1）也是一个S项.

定义6.3 S—公式的归纳定义如下：

（1）如果t0和t1都是S项，那么t0=t1是S—公式；

（2）如果t0，t1，…，tn-1都是S项而且R是S中的一个n元关系符号，那么R（t0，t1，…，tn-1）是一个S—公式；

（3）如果α是S—公式，那么⇁α也是S—公式；

（4）如果α和β是S—公式，那么（α∨β）也是S—公式；

（5）如果α是S—公式而且x是个体变项，那么∀xα和∃xα都是S—公式.

（6）一符号序列为S—公式当且仅当它由上面（1）～（5）的有穷多次应用而得.

由（1）和（2）导出的S—公式叫做原子公式.（3）至（5）决定的S—公式跟以前的意义相同.我们仍然可以用LS或WS表示全体S—公式，并称它为相应于符号集S的一阶语言，称S为它的符号集.

现在，要证明所有S项具有某个性质φ，只需证明：

（T1）每个个体变项都具有性质φ；

（T2）S中的每个个体常项都具有性质φ；

（T3）如果S项t0，t1，…，tn-1都有性质φ，并且f是S中的一个n元运算符号，那么f（t0，t1，…，tn-1）也具有性质φ.

同理，要证明所有S—公式都具有性质φ，现在只需证明：

（F1）每个形如t0=t1的S—公式有性质φ；

（F2）每个形如R（t0，t1，…，tn-1）的S—公式具有性质φ；

（F3）如果S—公式α具有性质φ，那么⇁α也有性质φ；

（F4）如果S—公式α和β具有性质φ，那么（α∨β）也有性质φ；

（F5）如果S—公式α有性质φ，并且x是一个个体变项，则∀xα和∃xα也都有性质φ.

定义6.4 var和sub的归纳定义如下：

var（x）={x}，var（c）=∅；

var（f（t0，t1，…，tn-1））=var（t0）∪var（t1）∪…∪var（tn-1）；

sub（t0=t1）={t0=t1}；

sub（R（t0，t1，…，tn-1））={R（t0，t1，…，tn-1）}；

sub（⇁α）={⇁α}∪sub（α）；

sub（（α∨β））={（α∨β）}∪sub（α）∪sub（β）；

sub（∀xα）={∀xα}∪sub（α）；

sub（∃xα）={∃xα}∪sub（α）.

定义6.5 公式α中的全体自由变项free（α）归纳定义如下：

free（t0=t1）=var（t0）∪var（t1）；

free（R（t0，t1，…，tn-1））=var（t0）∪var（t1）∪…∪var（tn-1）；

free（⇁α）=free（α）；

free（（α∨β））=free（α）∪free（β）；

free（∀xα）=free（α）-{x}；

free（∃xα）=free（α）-{x}.

上面的定义6.1至6.5都是有关语法的概念，下面的定义6.6至6.8跟语义有关.

定义6.6 一个S结构A就是具有下述性质的一个二元组（A，F）：

（1）A是一个非空集合，称为A的个体域或论域，A中的元素称为个体；

（2）F是符号集S上的一个映射；它满足下面的三个条件：

（i）对S中的每个n元关系符号R，F（R）是A上的一个n元关系；

（ii）对S中的每个n元运算符号f，F（f）是A上的一个n元运算；

（iii）对S中的每个常项c，F（c）是A的一个元素.

F（R），F（f）和F（c）也可记成R A，f A和c A，或者RA，f A和c A.当S有限时，如：S={R，f，c}，我们也可以用列举F的值的方法把S结构A=（A，F）写成A=（A，R A，f A，c A）.

关于个体指派和S解释的定义分别与第五章第五节中定义5.2和定义5.3完全一样，这里不再赘述.下面给出可满足关系的定义：

定义6.7 给定一个S解释Σ=（A，θ）.对于任一个S项t，Σ（t）的归纳定义如下：

（1）Σ（x）=θ（x）；

（2）Σ（c）=c A；

（3）Σ（f（t0，t1，…，tn-1））=f A（Σ（t0），Σ（t1），…，Σ（tn-1））.

定义6.7表明：任一个项t在S解释Σ下是A中的一个个体.

定义6.8 满足关系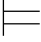的归纳定义如下：

对于原子公式、否定式、析取式和量词公式的情况，定义同第五章的定义5.4.(www.daowen.com)

有了定义6.7和6.8，我们可以定义其他一些语义概念.如：后承关系、有效性、可满足性和逻辑等值等等.相应的叠合引理可表述为：

引理（叠合引理） 令Σ1=（A1，θ1）是S1解释，Σ2=（A2，θ2）是S2解释，并且二者的个体域相同，即：A1=A2.令S=S1∩S2，那么：

（1）令t是一个S项，如果Σ1和Σ2对于出现在t中的S符号及个体变项的解释相同，则

Σ1（t）=Σ2（t）；

（2）令α是一个S—公式，如果Σ1和Σ2对于出现在α中的S符号以及α的自由变项的解释相同，则

归约结构和扩充结构的定义如前，有关的结果现在也成立.

联立代入的定义跟第五章第六节定义6.1稍有不同，即：只需增加下述两条：

另外，代入引理的表述与第五章第六节引理6.1完全一样，此处不再重复.

在FQC系统中增加如下有关等词的两条规则=+和=-，得到的系统记作FQC=.

在FQC=中，可证公式的定义完全类似于第五章第三节中的定义.

这里=+规则叫做等词引入规则，它反映演绎推理中这样的规则：它肯定个体域中的任何一个个体自己和自己完全相同.=-规则叫做等词消去规则，它反映了演绎推理中这样的规则：如果个体域中的个体a有某个性质，并且个体a和a′是等同的，那么a′也有这个性质.

要得到带等词的公理系统，我们只需在QC系统中附加下面的两个公式作为公理（模式）：

（1）t=t；

（2）t=t′→（α（t/x）→α（t′/x））.

这样得到的系统记作QC=.QC=系统与FQC=系统仍然是等价的.即：在FQC=中可证的公式一定在QC=中可证，在QC=中可证的公式，在FQC=中也可证.

可演绎性和相容性的定义分别与第六章第一节和第二节的定义一样.FQC=系统可靠性定理的证明跟FQC系统可靠性定理3.2的证明类似，只是在归纳步骤中多考虑了=+和=-两种情况.

最后，FQC=系统的完全性定理也是成立的.此证明可仿照本章第四节FQC系统完全性定理的证明去做，只是Henkin定理中的ΣΦ的构造需要修改一下，其他叙述都可照抄.ΣΦ的构造需作如下修改：

令Φ是含见证的极大相容集.首先，在全体S项上引进一个二元关系～：

t0～t1当且仅当t0=t1∈Φ

～是一个等价关系，而且相对于S中的运算符号和关系符号是同余的.也就是说，如果t0～t′0，t1～t′1，…，tn-1～t′n-1，那么对于S中的任一n元关系符号R和运算符号f，有其次，令[t]是t的等价类，等价类的全体记作TΦ.显然，TΦ是非空集.由Φ决定的项解释ΣΦ=（AΦ，θΦ）定义如下：

f（t0，t1，…，tn-1）～f（t′0，t′1，…，t′n-1），

R（t0，t1，…，tn-1）∈Φ当且仅当R（t′0，t′1，…，t′n-1）∈Φ.

（1）ΣΦ的个体域是TΦ；

（2）对S中的n元关系符号R有：

R AΦ（[t0]，[t1]，…，[tn-1]）当且仅当R（t0，t1，…，tn-1）∈Φ；

（3）对S中的个体常项c有，

c AΦ=[c]，即：c的等价类；

（4）对S中的n元运算符号f有：

（5）对各个个体变项x，有

θΦ（x）=[x]，

在项解释ΣΦ下，对于一切项t，我们有

ΣΦ（t）=[t]，

这样一来，每个项都被解释成它所属的等价类.至此，Henkin定理的证明可以完全照搬.

完全性定理仍然可以表述为：

（1）Φ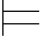α当且仅当Φ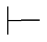α；

（2）Φ是可满足的当且仅当Φ是相容的.

用带等词和运算符号的一阶语言，可以很方便地把许多常见的数学理论形式化.下面我们给出两个简单的例子.

例6.1 第一章第三节偏序的定义3.15，现在可以形式化为：令S={R，=}：

（1）自返性：∀x R（x，x）；

（2）反对称性：∀x∀y（R（x，y）∧R（y，x）→x=y）；

（3）传递性：∀x∀y∀z（R（x，y）∧R（y，z）→R（x，z））.

例6.2 在数学理论——群论中，群的公理可以表示如下：

（g1）对一切x，y，z （x◦y）◦z=x◦（y◦z）；

（g2）对一切x x◦e=x；

（g3）对任一个x都有y使得： x◦y=e.

这里“◦”是群的乘法而“e”表示单位元（常元）.令S={◦，e}，则群的公理就可以形式地表示为：

（g1）′∀v0∀v1∀v2（v0◦（v1◦v2））=（v0◦（v1◦v2））；

（g2）′∀v0（v0◦e=v0）；

（g3）′∀v0∃v1（v0◦v1=e）.

令Φg={（g1）′，（g2）′，（g3）′}.在群论中，可以证明：

这就是左逆元存在定理.

最后，我们来扩充真值树方法，用以结束本节、本章以及本书的讨论.

在第二章里，我们介绍了真值树方法，其目的在于判断一个给定的公式是不是重言式.现在，将在真值树方法的基础上介绍一阶树方法.以便证明一个给定的一阶公式是逻辑有效的.

但是，由完全性定理知：每一个有效的公式都是可证公式.然而，从这个结论人们并不能找到一个能行的过程来决定：任一个公式是否是有效的.实际上已经证明：不存在决定一个公式是否有效或可证的能行过程，也就是说，狭谓词逻辑（与命题逻辑不一样）是不可判定的.

一阶树的构造与真值树的构造类似，二者不同之处在于，除了原来的三个命题规则（⇁⇁，∨，⇁∨）外，还需要补充四条量词规则，它们是：

在∀规则和⇁∃规则中，t可以是任意的项.在⇁∀规则和∃规则中，y是在正在扩张的分枝的任何公式中都不自由的任意变项，所以也称y为关键变项.

如果L是带等词“=”的语言，那么我们也承认以下三个等式规则.它们是：

SI规则：

这里的t是任意项.

这里f是L=的任一n元函项符号，t1，t2…，t2n是任意L项.

这里P是L=的任意n元谓词符号，t1，t2，…，t2n是任意L项.（特别地，当n=2时，P可以是=.）

SI规则叫做“自身恒等”规则，SF规则叫做“函项中的等量可替换性”规则，SP规则叫做“谓词中的等量可替换性”规则.

注意：这些等式规则总能用来扩张任一分枝，无论该分枝有什么公式.

一阶树和真值树的最后一个区别是：一阶树的一个分枝是封闭的，如果有一个原子公式α和⇁α都属于这个分枝的话.