本节我们证明:自然推理系统FQC和公理系统QC等价.即:一个公式α在FQC中是可证的,当且仅当它在QC中也是可证的.亦即:
定理 对于任意一个公式α,
证明 此证明分两步.第一步,(1)QC的公理都是FQC中的可证公式;(2)QC的推理规则是FQC的导出规则.
(1)QC的公理都是FQC中的可证公式.
(2)QC的推理规则是FQC的导出规则.即:当R1,R2和R3的前提是FQC的可证公式时,结论也一定是FQC的可证公式.
①如果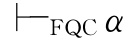 (y/x)→β,那么
(y/x)→β,那么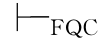 ∃xα→β,这里y不在∃xα和β中自由出现.
∃xα→β,这里y不在∃xα和β中自由出现.
②如果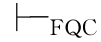 α→β(y/x),那么
α→β(y/x),那么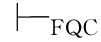 α→∀xβ,这里y不在∀xβ和α中自由出现.
α→∀xβ,这里y不在∀xβ和α中自由出现.
③如果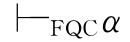 并且
并且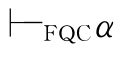 →β,那么
→β,那么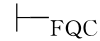 β.
β.
第二步:证明:凡FQC的可证公式都是QC的可证公式.
在QC系统中,要想证明一个公式可证是比较麻烦的.为此,我们采用下面的方法证明:FQC中的可证公式都是QC中的可证公式.
(1)我们在FQC中引进拟证明的概念.FQC中拟证明跟FQC中证明的概念的唯一区别是:拟证明允许直接引用QC的推理规则或引用QC的公理(包括定理)作为证明中的一步.由于QC中的可证公式都是FQC的可证公式(第一步证明的结论),因此在拟证明中引进QC的定理可以看成是引用Reit规则所产生的结果.也就是说,在该拟证明中先写下所引用定理的证明,然后再按Reit规则引入这些定理.又因为QC的推理规则都是FQC的导出规则,所以,用拟证明获得的结果仍然是FQC的可证公式.FQC中的任一个证明当然也是拟证明.
(2)我们证明FQC中的可证公式都是QC的可证公式的作法是:用QC的定理和推理规则R1至R3,将拟证明的子证明从最内层开始一步步地消除,最后得到QC的一个可证公式序列,而拟证明的结果仍是该序列的最后一个公式,从而是QC的可证公式.而最内层的子证明是指:在该拟证明中没有从属于它的子证明.
令π0是FQC的拟证明π的最内层的子证明,令
在π中用π′0替换π0,得到证明π′0.现在,我们用归纳法证明:通过在π′0的公式之间插入QC的一些定理,π′就可以转换成一个拟证明π″.
因为(φ1→φ1)是QC的定理,因此,它可以作为拟证明π″的一步而引入.
假定在公式(φ1→φ1),(φ1→φ2),…,(φ1→φi-1)之间都已经插入适当的公式.现在来考虑(φ1→φi),依据φ i在π中的由来,我们需要处理以下几种情况.
由于π0是π的最内层的子证明,φ i显然不能是引用⇁规则和→+规则得到的.所以,我们可以不考虑这两种情况.其他情形分别处理如下:
①如果φ i在π中是由Rep规则引入的,因此,在π″中(φ1→φi)仍是由Rep规则引入的公式.
②如果φ i在π中是由Reit规则引入的,此时在π″中可以先在(φ1→φi-1)下,由Rep规则或Reit规则引入φi,再在这个公式φ i下写上QC的定理(φi→(φ1→φi)),根据→-规则,可得:(φ1→φi).
③如果φ i在π中是作为QC的定理引入的,那么在(φ1→φi-1)之下,先写下QC的定理φi,然后再写上QC的定理:(φi→(φ1→φi)).最后,利用→-规则可得:(φ1→φi).
④如果φ i在π中是由→-规则引入的,此时有j,k<i使得φk=(φj→φi).因此,我们在公式(φ1→φi-1)和(φ1→φi)之间插入下面两个公式:
(i)(φ1→(φj→φi))→((φ1→φj)→(φ1→φi));
(ii)(φ1→φj)→(φ1→φi).
这里(i)是QC的定理,(ii)由(φ1→φk)(即:φ1→(φj→φk))和(i)用→-规则得到的.然后由(φ1→φj)和(ii)再用→-规则得:(φ1→φi).
⑤如果φ i在π中由∧+规则引入,此时有j,k<i使得φ i为(φj∧φk).在(φ 1→φi-1)和(φ1→φi)之间插入以下六个公式:
(i)φj→(φk→(φj∧φk));
(ii)(φj→(φk→(φj∧φk)))→((φ1→φj)→(φ1→(φk→(φj∧φk))));
(iii)(φ1→φj)→(φ1→(φk→(φj∧φk)));
(iv)φ1→(φk→(φj∧φk));
(v)(φ1→(φk→(φj∧φk)))→((φ1→φk)→(φ1→(φj∧φk)));
(vi)(φ1→φk)→(φ1→(φj∧φk)).
这里公式(i),(ii)和(v)都是QC的定理,(iii)是由(i)和(ii)用→-规则得到的,(iv)是由(φ1→φj)和(iii)用→-规则得到的.(vi)是由(iv)和(v)用→-规则得到的.最后,由(φ1→φk)和(vi)用→-规则可得:φ1→φi.
⑥如果φ i在π中是由∧-规则引入的,那么此时应当有公式ψ和小于i的j使得φ j为(φi∧ψ)或者(ψ∧φi).在(φ1→φi-1)和(φ1→φi)之间插入下面三个公式:
(i)(φi∧ψ)→φi(或者(ψ∧φi)→φi);
(ii)((φi∧ψ)→φi)→((φ1→(φi∧ψ))→(φ1→φi))
(或者((ψ∧φi)→φi)→((φ1→(ψ∧φi))→(φ1→φi)));
(iii)(φ1→(φi∧ψ))→(φ1→φi)(或者(φ1→(ψ∧φi))→(φ1→φi)).
这里公式(i)和(ii)都是QC的定理,(iii)是由(i)和(ii)用→-规则得到的.由(φ1→φj)(即:(φ1→(ψ∧φi))或(φ1→(φi∧ψ)))和(iii)用→-规则可得:(φ1→φi).
⑦如果φ i在π中是由∨+规则引入的公式,那么,应当有公式ψ和小于i的j使得φ i为(φj∨ψ)或者(ψ∨φj).此时,在公式(φ1→φi-1)和(φ1→φi)之间插入下列三个公式:
(i)(φj→(φj∨ψ))(或者(φj→(ψ∨φj)));
(ii)(φj→(φj∨ψ))→((φ1→φj)→(φ1→(φj∨ψ)))
(或者(φj→(ψ∨φj))→((φ1→φj)→(φ1→(ψ∨φj))));
(iii)(φ1→φj)→(φ1→(φj∨ψ))
(或者(φ1→φj)→(φ1→(ψ∨φj))).
这里的公式(i)和(ii)都是QC的定理,(iii)是由(i)和(ii)用→-规则得到的公式.
由(φ1→φj)和(iii)用→-规则可得:(φ1→φi).
⑧如果φ i在π中是由∨-规则引入的公式,那么,存在公式ψ1和ψ2和小于i的l,j.k使得:φ l为(ψ1∨ψ2),φ j为(ψ1→φi),φ k为(ψ2→φi).在(φi→φi-1)和(φ1→φi)之间插入下列九个公式:
(i)(ψ1→φi)→((ψ2→φi)→((ψ1∨ψ2)→φi));
(ii)((ψ1→φi)→((ψ2→φi)→((ψ1∨ψ2)→φi)))→((φ1→(ψ1→φi))→(φ 1→((ψ2→φi)→((ψ1∨ψ2)→φi))));(https://www.daowen.com)
(iii)(φ 1→(ψ1→φ i))→(φ 1→((ψ2→φ i)→((ψ1∨ψ2)→φ i)));
(iv)φ 1→((ψ2→φ i)→((ψ1∨ψ2)→φ i));
(v)(φ 1→((ψ2→φ i)→((ψ1∨ψ2)→φ i)))→(φ 1→(ψ2→φ i))→(φ 1→((ψ1∨ψ2)→φ i));
(vi)(φ 1→(ψ2→φ i))→(φ 1→((ψ1∨ψ2)→φ i));
(vii)φ 1→((ψ1∨ψ2)→φ i);
(viii)(φ 1→((ψ1∨ψ2)→φ i))→((φ 1→(ψ1∨ψ2))→(φ 1→φ i));
(ix)(φ 1→(ψ1∨ψ2))→(φ 1→φ i).
这里公式(i),(ii),(v)和(viii)都是QC的定理,(iii)由(i)和(ii)用→规则所得.(iv)是由(iii)和φ j用→-规则所得,(vi)是由(iv)和(v)用→-规则引入的.(vii)由(vi)和φ k用→-规则得到的.而(ix)是由(vii)和(viii)用→-规则得到的.由(ix)和φ l用→-规则可得:φ 1→φ i.
⑨如果φ i是在π中由↔+规则得到的公式,那么,存在公式φ,ψ和小于i的j,使得:φj是(φ→ψ)而φ k为(ψ→φ).因此,在(φ 1→φ i-1)和(φ 1→φ i)之间插入下列六个公式:
(i)(φ→ψ)→((ψ→φ)→(φ↔ψ));
(ii)(φ→ψ)→((ψ→φ)→(φ↔ψ))→((φ 1→(φ→ψ))→(φ 1→((ψ→φ)→(φ↔ψ))));
(iii)(φ 1→(φ→ψ))→(φ 1→((ψ→φ)→(φ↔ψ)));
(iv)φ 1→((ψ→φ)→(φ↔ψ));
(v)(φ 1→((ψ→φ)→(φ↔ψ)))→((φ 1→(ψ→φ))→(φ 1→(φ↔ψ)));
(vi)(φ 1→(ψ→φ))→(φ 1→(φ↔ψ)).
这里公式(i),(ii)和(v)都是QC的定理,(iii)是由(i)和(ii)用→-规则引入的,(iv)是由(iii)和φ j用→-规则引入的,(vi)是由(iv)和(v)用→-规则引入的.由(vi)和φ k用→-规则可得公式:φ 1→φ i.
⑩如果φ i在π中是用↔-规则得到的公式,那么,存在公式φ,ψ和小于i的j,使得:φ j为(φ↔ψ)而φ i为(φ→ψ)或(ψ→φ).在(φ 1→φ i-1)和(φ 1→φ i)之间插入下面三个公式:
(i)(φ↔ψ)→(φ→ψ)(或者(φ↔ψ)→(ψ→φ));
(ii)((φ↔ψ)→(φ→ψ)→((φ 1→(φ↔ψ))→(φ 1→(φ→ψ)))
(或者((φ↔ψ)→(ψ→φ))→((φ 1→(ψ↔φ))→(φ 1→(ψ→φ))));
(iii)((φ 1→(φ↔ψ))→(φ 1→(φ→ψ)))
(或者((φ 1→(ψ↔φ))→(φ 1→(ψ→φ)))).这里公式(i)和(ii)都是QC的定理,(iii)是由(i)和(ii)用→-规则得到的公式.由(iii)和(φ1 →φj )用→-规则可得公式:(φ 1→φi ).
⑪如果φi 在π中是由∀+ 规则引入的公式,那么,存在公式φ和个体变项x,y以及小于i的j使得:φi 为∀xφ,φj 为φ(y/x)并且y既不在∀xφ中自由出现也不在φ(y/x)所依赖的假设中自由出现.公式(φ1 →φi -1)和(φ1 →φi )分别是公式(φ1 →φ(y/x))和(φ 1→∀xφ);由于φ1 是φ(y/x)所依赖的假设,故y不在φ1 中自由出现.对公式(φ1 →φ(y/x))应用QC规则R2可得公式(φ 1→∀xφ),即,(φ 1→φi ).⑫
如果φi 在π中是由∀-规则引入的公式,那么,存在公式φ和项x,t以及小于i的j使得:φj 是公式∀xφ而φi 是φ(t/x).在公式(φ1 →φi -1)和(φ1 →φi )之间插入下面的三个公式:
(i)∀xφ→φ(t/x);
(ii)(φ 1→(∀xφ→φ(t/x)))→((φ 1→∀xφ)→(φ 1→φ(t/x)));
(iii)(φ 1→∀xφ)→(φ 1→φ(t/x)).
这里公式(i)和(ii)都是QC的定理,(iii)是由(i)和(ii)用→-规则得到的公式.由(iii)和(φ 1→φ j)用→-规则可得:(φ 1→φ i).
⑬如果φ i在π中是由∃+规则引入的公式,那么,存在公式φ和项x,t以及小于i的j使得:φ j为φ(t/x),而φ i为∃xφ.在公式(φ 1→φ i-1)和(φ 1→φ i)之间插入下面三个公式.
(i)φ(t/x)→∃xφ;
(ii)(φ(t/x)→∃xφ)→((φ 1→φ(t/x))→(φ 1→∃xφ));
(iii)(φ 1→φ(t/x))→(φ 1→∃xφ).
这里公式(i)和(ii)都是QC的定理,(iii)是由(i)和(ii)用→-规则得到的.由(iii)和(φ 1→φ j)用→-规则可得公式(φ 1→φ i).
⑭如果φ i在π中是由∃-规则得到的公式,那么存在公式φ和个体变项x,y以及小于i的j使得:φ j为∃xφ而φ k为(φ(y/x)→φ i),并且y既不在存在公式∃xφ和φ i中自由出现,也不在(φ(y/x)→φ i)所依赖的假设中自由出现.在公式(φ 1→φ i-1)和(φ 1→φ i)之间插入下面七个公式:
(i)(φ 1→(φ(y/x)→φ i))→(φ(y/x)→(φ 1→φ i));
(ii)φ(y/x)→(φ 1→φ i);
(iii)∃xφ→(φ 1→φ i);
(iv)(∃xφ→(φ 1→φ i))→(φ 1→(∃xφ→φ i));
(v)φ 1→(∃xφ→φ i);
(vi)(φ 1→(∃xφ→φ i))→((φ 1→∃xφ)→(φ 1→φ i));
(vii)(φ 1→∃xφ)→(φ 1→φ i).
这里公式(i),(iv)和(vi)都是QC的定理,(ii)是由(i)和公式(φ 1→φ k)用→-规则得到的.(iii)是(ii)应用QC规则R1得到的公式.(v)是由(iii)和(iv)应用→-规则引入的公式,而(vii)是由(v)和(vi)用→-规则得到的公式.由(vii)和公式(φ 1→φ j)用规则→-就可得到:φ 1→φ i.
至此,我们完成了在π0中引入φ i的各种情况.最后,我们还需要考虑(φ 1→φ i)的下一步是由→+和⇁规则引入的情况.如果(φ 1→φ n)的下一步是由→+规则引入的,则在(φ 1→φ n)之后的公式仍是(φ 1→φ n).因此,在π″中这个公式仍是(φ 1→φ n).因此,在π″中这个公式可以用Rep规则引入.如果(φ 1→φ n)的下一步是由⇁规则引入的,则公式φ 1应当是否定式⇁φ,而且存在小于i的j,k使得:φ j是⇁φ k,这下面的公式是φ.由上面的证明可知,我们在π″中已经引入(⇁φ→φ j)和(⇁φ→φ k).即:(⇁φ→⇁φ k)和(⇁φ→φ k).因此,在(φ 1→φ n)和φ之间插入下面两个公式:
(i)(⇁φ→φ k)→((⇁φ→⇁φ k)→φ);
(ii)(⇁φ→⇁φ k)→φ.
这里公式(i)是QC的定理,(ii)是由(i)和(φ 1→φ k)用→-规则得到的公式.由(ii)和(φ 1→φ j)用→-规则就可在π″中引入φ.
这样一来,我们就把π′转换成了一个拟证明π″,而π″的最内层子证明的个数比π的少一个.继续上面的过程有穷多次,我们就可以把π的所有最内层的子证明消除掉,从而得到一个拟证明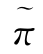 ,当对
,当对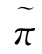 进行上述同样转换时,除了要处理上述各种情况,还要处理由QC的R1和R2规则引入的情形.但是,这些都不困难,从而略去细述.至此,我们完成了定理的证明.
进行上述同样转换时,除了要处理上述各种情况,还要处理由QC的R1和R2规则引入的情形.但是,这些都不困难,从而略去细述.至此,我们完成了定理的证明.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







