定义6.2 一个一阶公式α被称为前束范式，如果它形如

Q0 x0 Q1 x1…Qn-1 xn-1β，

这里n≥1并且对每个i（i=0，1，…，n-1），Qi是∀或∃，公式β中不含量词.符号序列Q0 x0 Q1 x1…Qn-1 xn-1称为前束词，β称为α的母式或基式.

例6.5 公式

和公式

都是前束范式.

同命题逻辑中的结论一样，我们有关于前束范式存在定理.即：对于狭谓词逻辑中的每一个公式，都可以找到一个与之逻辑等值的前束范式，并且二者的自由变项相同.一个公式的前束范式不是唯一的.

前束范式存在定理的证明过程，实际上给出了求一个公式的前束范式的步骤.因此，下面我们先证明前束范式存在定理，然后给出求前束范式的步骤，最后举例说明如何寻找前束范式.

在证明前束范式存在定理之前，先证明逻辑等值“～”具有下面的性质：

（1）α～α；

如果α～β并且β～γ，那么α～γ；

如果α～β，那么β～α.

（2）如果α～β并且γ～δ，那么

⇁α～⇁β，（α∧γ）～（β∧δ），

∀xα～∀xβ，∃xα～∃xβ.

（3）⇁∀xα～∃x⇁α，⇁∃xα～∀x⇁α.

（4）如果x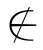free（β），那么

（∀xα∧β）～∀x（α∧β），（∀xα∨β）～∀x（α∨β），

（β∧∀xα）～∀x（β∧α），（β∨∀xα）～∀x（β∨α），

（∃xα∧β）～∃x（α∧β），（∃xα∨β）～∃x（α∨β），

（β∧∃xα）～∃x（β∧α），（β∨∃xα）～∃x（β∨α）.

（5）如果y不在∀xα或∃xα中自由出现，那么

∀xα～∀yα（y/x），∃xα～∃yα（y/x）.

性质（1）～（4）的证明留给读者完成.性质（5）的证明如下：

对任意的解释Σ，Σ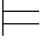∀yα（y/x）

当且仅当 对一切a∈A，Σ（a/y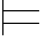）α（y/x）

当且仅当 对一切a∈A，Σ（a/y）（Σ（a/y）（y）/x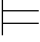）α

（代入引理）

当且仅当 对一切a∈A，Σ（a/y）（a/x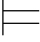）α

当且仅当 对一切a∈A，Σ（a/x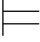）α（叠合引理）

当且仅当 Σ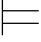∀xα.

对任意的解释Σ，Σ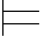∃yα（y/x）

当且仅当 有a∈A，Σ（a/y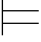）α（y/x）

当且仅当 有a∈A，Σ（a/y）（Σ（a/y）（y）/x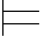）α（代入引理）

当且仅当 有a∈A，Σ（a/y）（a/x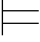）α

当且仅当 有a∈A，Σ（a/x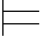）α（叠合引理）

当且仅当 Σ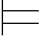∃xα.

因此，∀xα～∀yα（y/x）并且∃xα～∃yα（y/x）.

性质（5）刻画了约束变项的一个重要特征.即：公式中的约束变项可以改名，改名后的结果与原公式逻辑等值.

引理6.2 如果公式α中至少含有一个量词，那么α逻辑等值于一个形如Qxβ的公式，公式β中所含量词的个数比α少一个，这里的Q是∀或是∃.

证明 施归纳于公式α的结构：

由于α至少含有一个量词，因此，α不能是原子公式.

设α=⇁β并且结论对β成立.那么，β逻辑等值于一个形如（Qx）β1的公式，β1所含量词个数比β少一个，这里的Q或是∀或是∃.利用性质（2）和（3）可知，α～（Q′x）⇁β1，这里

⇁β1所含量词的个数与β1相同，因此比β少一个量词，所以也比⇁β少一个量词.Q′x⇁β1即为所求.

设α=（β∨γ）并且结论对β和γ都成立.由于α至少含有一个量词，因此，β和γ中至少有一个含有一个量词.不妨设β中至少含有一个量词（当γ至少含有一个量词时，证明是类似的）.由归纳假设、结论对β成立可知：存在x和公式β1使得β～Qxβ1，其中β1所含量词的个数比β少一个，Q是∀或是∃.任取一个既不在γ中又不在Qxβ1中出现的个体变项y，根据逻辑等值的性质（5）和（4），有：

和 α～Qy（β1（y/x）∨γ）.(www.daowen.com)

设α=Qxβ，结论显然成立.

定理（前束范式存在定理） 对于狭谓词逻辑中的每一个公式α，都可以找到一个与之逻辑等值的前束范式β，并且二者的自由变项相同.

证明 施归纳于公式α所含量词的个数n.

当n=0时，α本身就是一个前束范式，结论显然成立.

当n＞0时，α中至少含有一个量词.因此根据引理6.2，有x和β，使得α～Qxβ，β中所含量词的个数比α中少一个，这里的Q或是∀或是∃.对β而言，由归纳假设，存在一个前束范式β1，使得β～β1而且β1的自由变项的个数跟β的相同.利用逻辑等值～的性质，可得：

Qxβ～Qxβ1，

和 α～Qxβ1.

这里Qxβ1即为所求的前束范式.

从引理6.2和前束范式存在定理的证明过程中，我们可以获得寻找一个与已知公式逻辑等值的前束范式的方法.

求一个公式的前束范式的步骤如下：

第一步：利用

（α→β）～（⇁α∨β），

和 （α↔β）～（（α→β）∧（β→α）），

消去逻辑联结词→和↔.

第二步：利用

⇁⇁α～α，⇁（α∧β）～（⇁α∨⇁β），

⇁（α∨β）～（⇁α∧⇁β），⇁∀xα～∃x⇁α，

和 ⇁∃xα～∀x⇁α

把否定号⇁深入到原子公式之前或消去.

第三步：必要时，把约束变项改名.

第四步：利用～的性质（4），把量词移到整个公式的最前面，从而得到一个前束范式.

例6.6 求公式∀v0 P（v0）→∃v0 Q（v0）的前束范式.

解 消去→，得

⇁∀v0 P（v0）∨∃v0 Q（v0），

⇁深入，得

∃v0⇁P（v0）∨∃v0 Q（v0），

约束变项改名，得

∃v0⇁P（v0）∨∃v1 Q（v1），

量词前移，得

∃v0∃v1（⇁P（v0）∨Q（v1）），

此式即为所求.

例6.7 求∃x∀y R（x，y）→∃zS（x1，z）的前束范式.

解 消去→，得

⇁∃x∀y R（x，y）∨∃zS（x1，z），

⇁深入，得

∀x∃y⇁R（x，y）∨∃zS（x1，z），

量词前移，得

∀x∃y∃z（⇁R（x，y）∨S（x1，z）），

此式即为所求.

由于依不同次序将量词前移，还可以得到以下不同（但是等值）的前束范式：

∀x∃z∃y（⇁R（x，y）∨S（x1，z）），

∃z∀x∃y（⇁R（x，y）∨S（x1，z）），

∃z∃y∀x（⇁R（x，y）∨S（x1，z））.

所以，与一个公式逻辑等值的前束范式不唯一.