1.证明下面的公式是逻辑等值的：

（1）（α∧β）和⇁（⇁α∨⇁β）；

（2）（α∨β）和⇁（⇁α∧⇁β）；

（3）（α→β）和（⇁α∨β）；

（4）（α↔β）和（α→β）∧（β→α）；

（5）（α↔β）和⇁（α∨β）∨⇁（⇁α∨⇁β）；

（6）（α↔β）和（α∧β）∨（⇁α∧⇁β）；

（7）∀xα和⇁∃x⇁α.

2.指出下列公式是否逻辑有效式，并加以证明：

（1）∀x（α→β）→∃xα→∃xβ；

（2）（∀xα→∀xβ）→∀x（α→β）；

（3）∃x（α∧β）→∃xα∧∃xβ；

（4）∃xα∧∃xβ→∃x（α∧β）；

（5）∀x（α∨β）→∀xα∨∀xβ；

（6）∀xα∨∀xβ→∀x（α∨β）.

3.证明：如果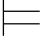α↔β并且公式γ′是以β替换公式γ中所有形如α的子公式而得，则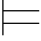γ↔γ′.（提示：施归纳于γ的结构.）

4.证明下面的公式逻辑等值：

（1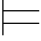）∀x（α∧β）↔∀xα∧β；

（2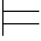）∃x（α∧β）↔∃xα∧β；

（3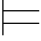）∀x（α∨β）↔∀xα∨β；

（4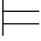）∃x（α∨β）↔∃xα∨β；

（5）∀x（α→β）↔∀xα→β；

（6）∃x（α→β）↔∀xα→β；

（7）∀x（β→α）↔β→∀xα；

（8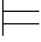）∃x（β→α）↔β→∃xα.

在（1）～（8）中，x不在β中自由出现.

5.证明：Φ，α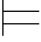β当且仅当Φ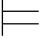α→β，从而证明：(www.daowen.com)

6.设Σ=（A，θ），其中A=（N，≤），“≤”是自然数集N上的小于等于关系，θ是N上的恒等映射.证明Σ是以下{R}—公式的模型：

（1）∀x∀y∀z（R（x，y）∧R（y，z）→R（x，z））；

（2）∀x∀y（R（x，y）∨R（y，x））.

7.证明：如果x不在α中自由出现，则α，∀xα及∃xα都是逻辑等值的.

8.构造一个仅含逻辑符号（即只有关系符号=）的闭公式α，使得α在解释Σ中成立，当且仅当个体域A中

（1）至少有三个元素；

（2）至多有三个元素；

（3）恰好有三个元素.

9.只用一个二元关系符号构造一个闭公式α，使α没有有穷模型（即个体域有穷），但当A是任何无穷集时，则α就有一个以A为个体域的模型.

10.对于下列四个公式和两个解释，如果一公式是句子，指出它是真的还是假的；如果一公式不是句子，指出对其中所含自由变元指派以什么样的值，它才是真的.

（1）R（f（v1，v2），e）；

（2）∀v1 R（f（v1，v2），e）；

（3）R（v1，v2）→⇁R（v2，v1）；

（4）∀v1∀v2∀v3（R（v1，v2）→（R（v1，v3）→R（v2，v3）∨R（v3，v2）））.

①论域是所有正整数的集合，R（x，y）为x≥y，f（x，y）为x·y，e=1；

②论域是所有整数集的集合，R（x，y）是x⊂y（即x真包含于y），f（x，y）是x∩y，e为空集.

11.下列公式在所给解释下表示论域上的什么关系（或性质）.

（1）令R（v3，v4）：∃v1∃v2（P（v1，v3）∧P（v2，v4）∧Q（v1，v2））；

论域是人的集合，P（x，y）表示x是y的母亲，Q（x，y）表示x是y的姐妹.

（2）令P（v2）：∀v1（⇁R（v1，e）→R（f（v1，v2），g（e））），

论域是所有有理数的集合，R（x，y）表示x=y，f（x，y）表示x·y，g（x）=x+1，e=0.

12.分别给出满足和不满足下列公式的解释：

（1）∃v1 R（v1，f（v2，v2））；

（2）R（v1）∧∀v2⇁Q（v1，v2）；

（3）∀v1∀v2（R（v1，v2）↔∃v3 Q（v1，v2，v3））.

13.试只用一个二元关系符号（不用其他非逻辑符号），构造L句子α和β，使得α在任何具有有穷论域的解释下都为假，但可以在一个具有无穷论域的解释下为真；β在任何具有有穷论域的解释下都真.但在一个具有无穷论域的解释下为假.（提示：考虑在自返性、传递性和承接性（即是否对论域中的每一个体μ都有一个个体μ′，使得μ与μ′有所说关系）上有其特点的两个二元关系.）