对于一个形式系统，不仅仅要研究它本身的语法规律，更重要的是给形式系统赋予一种含义，使抽象的符号变成有内容的语句.这也正是莱布尼茨最初设想的要建立一种表意的符号语言.因而探求形式系统的含义和解释符号序列的内容是这一节的主要研究内容.

通常，对于一个给定的符号集S，首先要确定一个个体域，然后把S中的常项和关系（谓词）符号分别解释成该个体域中的个体和个体间的关系.这样，才能使S—公式具有一定的含义.闭公式在这种解释下，是具有一定含义的命题.对于含自由变项的公式，如果希望它表示命题，就需要对其中的自由变项指定个体.也就是说，只有在对其中的自由变项指定某个个体以后，它才表示命题.怎样确定个体域和解释个体间的关系是相当自由的，下面将通过几个具体的例子来说明.

例5.1 令R是一个二元关系符号，设{R}—公式为：

假定取全体集合组成的类V为个体域，“∃v0”表示“有一个集合x”，“∀v1”表示“对任意的集合y”，R被解释为V上的属于关系∈，那么（1）式表示下面的命题：

“存在一个集合x，使得对任意的集合y，y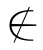x.”

只要取集合x为空集∅，这个命题在集合论中就是一个真命题.此时称公式（1）在（V，∈）中成立.

例5.2 令R是一个二元关系符号，{R}—公式为：

假定取全体自然数集N为个体域，“∀v0”表示“对任一个自然数n”，“∃v1”表示“有一个自然数m”，并把R解释为N上的小于关系＜，那么（2）式表示下面的命题：

“对任一个自然数n都有一个自然数m，使得n＜m.”

因为对任意的自然数n，只要取m=n+1，上述命题就成立.因此，这个命题在初等数论中是一个真命题.此时也称公式（2）在（N，＜）中成立.

但是，如果取全体负整数的集合Z-作为个体域，R仍被解释为小于关系＜，那么（2）式表示下面的命题：

“对于任一负整数k有一个负整数l，使得k＜l.”

因为在全体负整数的集合Z-中，不存在比-1还大的负整数，因此，该命题在初等数论中是一个假命题.此时我们称公式（2）在（Z-，＜）中不成立.

例5.3 令R仍然是一个二元关系符号，{R}—公式为：

在（N，＜）中是否表示一个命题，只有在对（3）式中的自由变项指定自然数.例如，对v0和v1分别指定6和8，那么（3）式就表示下面的真命题：

“如果6＜8，则有一个自然数n，使得6＜n并且n＜8.”

显然n=7即可.如果对v0和v1分别指定6和7，那么（3）式表示下面的假命题：

“如果6＜7，则有一个自然数n，使得6＜n并且n＜7.”

显然n不存在.

下面将给出解释的精确定义，同时也将定义一个解释什么时候产生一个真（或假）的命题.由于这一节引进的概念都与符号序列所指的意义有关，因此把这些概念叫做语义概念.在下面的讨论中，将沿用第一章中的一些符号和记法.

定义5.1 一个S结构A就是具有下面性质的一个二元组（A，F）：

（1）A是一个非空集，称为A的个体域或论域，A中的元素称为个体；

（2）F是符号集S上的一个映射，它满足：

①对S中每个n元关系符号R，F（R）是A上的一个n元关系；

②对S中每个个体常项c，F（c）是A中的一个个体.

注意：定义中的①对S中的每个n元关系符号R指定A上的一个n元关系F（R），即F（R）⊆An.另外，F（R）和F（c）常被分别记作R A和c A.

约定：用A，B，…分别表示结构A，B，…的个体域，还把S结构A=（A，F）用列举F值的方法来代替F.例如，{R，c}结构可以记作A=（A，R A，c A）.在前面例5.1中，{R}结构A=（V，F）也可以记作（V，∈V），即（V，∈）.例5.2中的{R}结构A=（N，F），即（N，＜）或者（Z-，＜）.

定义5.2 一个S结构A的一个个体指派（简称指派）是全体个体变项到A的个体域A的一个映射θ，也就是说，θ对每个个体变项指定一个个体.亦即，对一切x，θ（x）∈A.

定义5.3 一个S解释Σ就是由S结构A和A的一个指派θ组成的一个二元有序组（A，θ）.

对于给定的符号集S来说，在不致于混淆的情况下，常把S结构和S解释分别简称为结构和解释.

如果θ是A的一个指派，a∈A并且x是一个个体变项，那么θ（a/x）是如下定义的一个指派：

即：指派θ（a/x）除了对x指定a外，其余都跟θ相同.当Σ=（A，θ）时，令

Σ（a/x）=（A，θ（a/x））.

例5.4 令S={R}，R是一个二元关系符号，令Σ=（A，θ），其中A=（N，≥），θ为自然数集N上的恒等映射，“≥”是N上的大于等于关系，则{R}—公式为：

现在可以被分别解释为：

因此，例5.4中的“≥”关系为自然数集N上的线序关系.这是自然数域上的算术真理.

如果将R解释为N上的小于关系＜，则{R}—公式（1）和（2）在Σ′=（（N，＜），θ）下被分别解释为：

此时，公式（3′）成立而公式（4′）不成立，因为并不是任意的两个自然数x和y满足x＜y或者y＜x.除此之外，还有相等关系.因此，可以说{R}—公式（1）和（2）在给定的解释Σ下均为真，而在给定的解释Σ′下一个是真命题另一个是假命题.

一般地，给定一个S解释，任一S—公式都表示一个命题.如何确定这些命题在所给解释下的真假，可以用下面的定义来判断.

定义5.4（可满足关系的定义） S解释Σ=（A，θ）满足S—公式α，记作Σ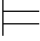α，其归纳定义如下：

（1）Σ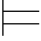R（t0，t1，…，tn-1）当且仅当R A（Σ（t0），Σ（t1），…，Σ（tn-1））成立（即：R A对Σ（t0），Σ（t1），…，Σ（tn-1）成立），这里Σ（ti）定义如下：

（2）Σ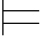⇁α当且仅当Σ 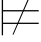α（即：Σ不满足α）；

（3）Σ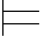（α∨β）当且仅当Σ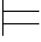α或者Σβ；

（4）Σ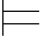∀xα当且仅当对一切a∈A，Σ（a/x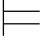）α，

Σ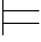∃xα当且仅当有一个a∈A，Σ（a/x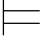）α.

当Σ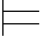α成立时，也称Σ是α的一个模型或者α在Σ中成立.

令Φ是一个公式集，如果Σ满足Φ中的每个公式，那么称Σ是Φ的一个模型，记作Σ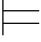Φ.

由定义5.4可得：

定义5.4看起来比较复杂，但实际应用起来还是很方便的.下面举例说明它的使用.

例5.5 考虑{R}—公式：∃v1 R（v0，v1）.

结构A=（N，＜），A中的指派θ为对一切个体变项x，θ（x）=8.对于这一{R}解释Σ=（A，θ），有

即：有一个n∈N，使得

Σ（n/v1）（v0）＜Σ（n/v1）（v1） 当且仅当 有一个n∈N，使8＜n.

因为只需取n=9，就有8＜n成立.所以，Σ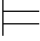∃v1 R（v0，v1）.

例5.6 考虑本节例5.1中的{R}—公式

∃v0∀v1⇁R（v1，v0）.

结构A=（V，∈），A中的指派θ取V上的恒等映射，对于这一{R}解释Σ=（A，θ），有

当且仅当 有一个a∈V并且对一切b∈V，使得

当且仅当 有一个a∈V并且对一切b∈V，使得

当且仅当 有一个a∈V并且对一切b∈V，使得

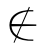（Σ（a/v0）（b/v1）（v1），Σ（a/v0）（b/v1）（v0））.

即：有一个a∈V并且对一切b∈V，

Σ（a/v0）（b/v1）（v1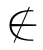）Σ（a/v0）（b/v1）（v0），

当且仅当 有一个a∈V并且对一切b∈V，b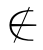a.

因为只需取a=∅，对一切b∈V，有b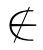∅成立.所以，

例5.7 考虑本节例5.4中的{R}—公式

结构A=（N，＜），A中的指派θ取N上的恒等映射.对于这一{R}解释Σ=（A，θ），有

当且仅当 对任意的n1，n2，n3∈N，使得

当且仅当 对任意的n1，n2，n3∈N，如果

则

当且仅当 对任意的n1，n2，n3∈N，如果

并且

则

即：对任意的n1，n2，n3∈N，如果亦即：对任意的n1，n2，n3∈N，如果n1＜n2，并且n2＜n3，则n1＜n3成立.所以，

但是，如果Σ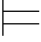∀x∀y（R（x，y）∨R（y，x））

当且仅当 对一切n，m∈N，有

当且仅当 对一切n，m∈N，有

当且仅当 对一切n，m∈N，有

Σ（n/x）（m/y）（x）＜Σ（n/x）（m/y）（y）

或者

Σ（n/x）（m/y）（y）＜Σ（n/x）（m/y）（x）

即：对一切n，m∈N，n＜m或者m＜n.

因为对任意两个自然数n和m，当n=m时，n＜m或m＜n均不成立.所以：

利用可满足的概念，我们可以将命题逻辑中的重言后承、可满足性和重言等值等概念进行拓展.在下面的定义中，假定S是一个固定的符号集，我们有：

定义5.5 （1）称公式α是公式集Φ的一个逻辑后承，如果每一个满足Φ的解释也满足α，记作Φ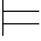α.特别地，当Φ={β}时，将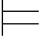{β}α简记作β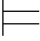α.而Φ∪{β}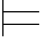α简记作Φ，β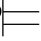α.(www.daowen.com)

（2）称公式α是逻辑有效的，如果它是空集的逻辑后承，即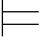：∅α，记作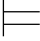α.即：对任意的解释Σ，Σ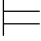α.

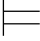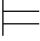（3）称公式α和β是逻辑等值的，如果它们互为逻辑后承，即：αβ并且βα，记作

（4）称公式α是可满足的，如果有一个解释Σ满足α，记作satα；称公式集Φ是可满足的，如果有一个解释Σ满足Φ中每一个公式，记作satΦ.

例5.8 QC的公理A1至A6是逻辑有效的.

证明 （1）A1：α∨α→α.

假设有一个解释Σ，使得

故：对任意的解释Σ，都有Σα∨α→α.所以，公理A1是逻辑有效的.

（2）容易证明：A2和A3也是逻辑有效的.

（3）证A4也是逻辑有效的.

假设有一个解释Σ，使得

则Σ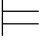（β→γ）并且Σ 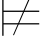（α∨β→α∨γ）.

由此可得：Σ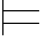（β→γ）并且Σ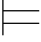（α∨β）并且Σ 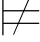（α∨γ）.

由此可得：Σ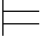（β→γ）并且Σ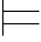（α∨β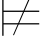）并且Σ α并且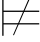Σ γ.由Σ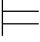（α∨β）且Σ 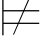α可得：Σβ.

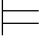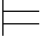由Σβ并且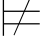Σ γ可得：Σ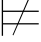 （β→γ）.矛盾.故：对任意的解释Σ，都有：

所以，公理A4逻辑有效的.

（4）证A5也是逻辑有效的.

假设有一个解释Σ，使得

由此得：Σ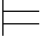∀xα并且Σ 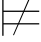α（y）.利用定义4.4可得：对一切a∈A，Σ（a/x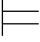）α，但由代入引理可得：

矛盾.故：对任意的解释Σ，都有：

所以，公理A5是逻辑有效的.

公理A6的有效性证明，类似于（4），从而详细证明略.

引理5.1 对任意的公式α和β，{α，α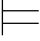→β}β.

证明 由定义5.5易证.

引理5.2 对任意的公式集Φ和任意的公式α，Φ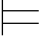α当且仅当Φ∪{⇁α}不可满足.特别地，α逻辑有效当且仅当⇁α不可满足.

证明 Φα，当且仅当，每一个满足Φ的解释也满足α，当且仅当没有一个满足Φ的解释不满足α，当且仅当没有一个解释满足Φ∪⇁α，当且仅当Φ∪⇁α不可满足.

公式α和β是逻辑等值的，（记作：α～β）当且仅当它们在相同的解释下是逻辑有效的，即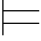α↔β成立.在前面的一节里，已经知道下面的各对公式是可证等值的，从而不难证明它们也是逻辑等值的.

（1）（α∧β）和⇁（⇁α∨⇁β）；

（2）（α∨β）和⇁（⇁α∧⇁β）；

（3）（α→β）和（⇁α∨β）；

（4）（α→β）和⇁（α∧⇁β）；

（5）（α↔β）和（α→β）∧（β→α）；

（6）（α↔β）和⇁（α∨β）∨⇁（⇁α∨⇁β）；

（7）（α↔β）和（α∧β）∨（⇁α∧⇁β）；

（8）∀xα和⇁∃x⇁α；

（9）∃xα和⇁∀x⇁α.

特别地，如果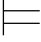（α↔β）并且公式γ′是以β替换公式γ中所有形如α的子公式而得，则（γ↔γ′）.证明留给读者完成.

下面的结论表明，S—公式α和S解释Σ之间的满足关系Σ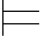α仅仅依赖于对α中所含的自由变项、个体常项和关系符号所作的解释.

引理5.3（叠合引理） 令Σ1=（A1，θ1）是S1解释，Σ2=（A2，θ2）是S2解释，二者的个体域相同（即A1=A2），并且令S=S1∩S2.如果Σ1和Σ2对于S—公式α的自由变项和出现在α中的S符号作出的解释相同（或者说：Σ1和Σ2对于S—公式α的自由变项和出现在α中的S符号是一致的），那么Σ1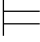α当且仅当Σ2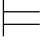α.

证明 施归纳公式于α的结构.

Σ1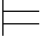R（t0，t1，…，tn-1）当且仅当R A1（Σ1（t0），Σ1（t1），…，Σ1（tn-1））

当且仅当R A1（Σ2（t0），Σ2（t1），…，Σ2（tn-1））

（归纳假设）

当且仅当R A2（Σ2（t0），Σ2（t1），…，Σ2（tn-1））

当且仅当Σ2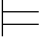R（t0，t1，…，tn-1）；

Σ1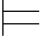⇁β当且仅当Σ1 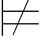β

当且仅当Σ2 β（归纳假设）

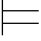当且仅当Σ2⇁β；

Σ1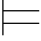（β∨γ）当且仅当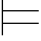Σ1β或者Σ1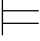γ

当且仅当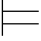Σ2β或者Σ2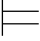γ（归纳假设）

当且仅当Σ2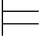（β∨γ）；

Σ1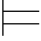∀xβ当且仅当对一切a∈A1，Σ1（a/x）β

当且仅当对一切a∈A2，Σ2（a/x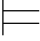）β（归纳假设）

当且仅当Σ2∀xβ；

Σ1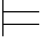∃xβ当且仅当有一个a∈A1，Σ1（a/x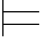）β

当且仅当有一个a∈A2，Σ2（a/x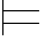）β（归纳假设）

当且仅当Σ2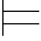∃xβ.

（注意：在证明含有量词的公式时，归纳假设能应用于β和Σ1（a/x）以及Σ2（a/x），是由于free（β）⊆free（α）∪{x}，而解释Σ1（a/x）和Σ2（a/x）对于出现在β中的一切符号和所有自由变项的解释相同.）

定义5.6 令S和S′都是符号集并且S⊆S′；令A=（A，F）是一个S结构，而A′=（A′，F′）是一个S′结构.称A是A′的一个S归约（简称归约），当且仅当A=A′并且F和F′对于S中任一符号的解释都相同.此时，也称A′为A的一个扩充，记作A=A′↾S.

关于解释、后承和可满足性等概念的定义都是在一个固定的符号集S上而作的.下面的引理表明，这样的要求不是必要的.

引理5.4 令Φ是一个公式集并且S⊆S′，则Φ相对于S是可满足的当且仅当Φ相对于S′是可满足的.

证明 如果Σ′=（A′，θ′）是一个S′解释并且Σ′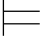Φ，那么由叠合引理可知，S解释（A′↾S，θ′）是Φ的一个模型.

另一方面，如果Σ=（A，θ）是满足Φ的一个S解释，我们可以把A扩充成一个S′结构A′使得A′↾S=A（由于对S′-S中的符号可以随意解释）.根据叠合引理可知，S′的解释（A′，θ）是Φ的一个模型.

最后，我们把Σ（a/x）的定义推广如下：

定义5.7 令x0，x1，…xr两两不相同，Σ=（A，θ）是一个解释，a0，a1，…，ar∈A，那么A中的指派θ（a0/x0，a1/x1，…，ar/xr）和解释Σ（a0/x0，a1/x1，…，ar/xr）的定义如下：

这里需要注意的是：在本章中我们所做的一些工作都是在第三章命题逻辑的基础上的扩充.以此类推，一阶语言的语义也应该是命题语义的扩充，或者说是在真值赋值σ的基础上定义一阶语言的语义.但从本节的内容上看，定义的解释Σ与真值赋值σ似乎没有任何联系.其实，只需解读定义5.4即可.首先将记号Σ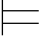α理解为αΣ=1.于是，由Σ 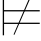α可得αΣ=0.因此，定义5.4等价于下面的定义5.4′.

定义5.4′ 一个S—公式α在S解释Σ下的值αΣ归纳定义如下：

（1）如果R是S的一个n元非逻辑关系符号，t0，t1，…，tn-1都是S项，那么

（2）对每一个S—公式β，

（3）对S—公式β和γ，

（4）对每一个S—公式β和自由变项x，

这里的A是Σ的论域.

这样以来，Σ满足公式α当且仅当αΣ=1.其实，也可以称Σ为赋值，记作：Σ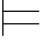α.或者换一种记法，将定义5.1中的映射F和定义5.2中的个体指派θ毗连起来，得到一个新的映射，称之为赋值，并记作σ.即：

这样以来，定义5.4又可以重述为：

定义5.4″ 一个S—公式α在赋值σ下的值定义如下：

（1）如果α是原子公式R（t0，t1，…，tn-1），那么

（2）如果α是否定式⇁β，那么

（3）如果α是析取式（β∨γ），那么

（4）如果α是∀xβ或∃xβ，那么

这里的A是σ的论域.

其实，解释Σ和赋值σ都依赖于个体指派θ.因为有一个θ，就已经有一个S结构A.因此，A中的映射F也就确定了.对σ也一样.这样一来，就可以将解释看成真值赋值的一种扩充.我们称这种扩充为赋值，在不引起混淆的情况下，仍记作σ.