（1）
∀xα→α.
证明
（2）
α→∀xα，x不在α中自由出现.
证明
由于x不在α中自由出现，当然更不会在∀xα中自由出现，所以我们可以使用∀+规则.
（3）
α↔∀xα，x不在α中自由出现.
证明
（4）
α→∃xα.
证明
（5）
∃xα→α，x不在α中自由出现.
证明
由于x不在α中自由出现，当然更不会在∃xα中自由出现，所以我们可以使用∃-规则.
（6）
α↔∃xα，x不在α中自由出现.
证明 由（4）和（5）可得.
（7）
∀xα→∃xα.
证明
（8）
∃xα→∀xα，x不在α中自由出现.
证明
由于x不在α中自由出现，当然更不会在∃xα和∀xα中自由出现，因此∃-和∀+规则在这里都可以使用.
（9）
∀xα↔∃xα，x不在α中自由出现.
证明 由（7）和（8）可得.
从（3），（6）和（9）中可以看出：对于不在一个公式中自由出现的个体变项，用全称量词修饰和不用量词修饰，用存在量词修饰和不用量词修饰，以及用全称量词修饰和用存在量词修饰所得结果都是可证等值的.
（10）
∀x∀yα→∀y∀xα.
证明
（11）
∃x∃yα→∃y∃xα.
证明
（12）
∃x∀yα→∀y∃xα.
证明
（10），（11）和（12）刻画了重叠量词的特征.（10）和（11）中的→可以换成↔，由此可得：同名的量词可以任意交换，交换后所得的结果跟原公式仍然是可证等值的.但是，（12）中的→不能换成↔.由此可得：不同名的量词不能任意交换.否则，交换后的结果跟原公式不是可证等值的.
（13）
∀x（α∧β）→∀xα∧∀xβ.
证明
（14）
∀xα∧∀xβ→∀x（α∧β）.
证明
（15）
∀x（α∧β）↔∀xα∧∀xβ.
证明 由（13）和（14）可得.
（16）
∀x（α∧β）→α∧∀xβ.
证明
（17）
α∧∀xβ→∀x（α∧β），x不在α中自由出现.
证明
（18）
∀x（α∧β）↔α∧∀xβ，x不在α中自由出现.
证明 由（16）和（17）可得.
（19）
∀x（α∧β）↔∀xα∧β，x不在β中自由出现.
证明 证法同（16），（17）和（18）.
（15）是全称量词对于合取的分配律.（18）和（19）分别是全称量词对合取的右和左的移置律.
（20）
∃x（α∧β）→∃xα∧∃xβ.
证明
（21）
∃x（α∧β）→∃xα∧β，x不在β中自由出现.
证明
（22）
∃xα∧β→∃x（α∧β），x不在β中自由出现.
证明
（23）
∃x（α∧β）↔∃xα∧β，x不在β中自由出现.
证明 由（21）和（22）可得.
（24）
∃x（α∧β）↔α∧∃xβ，x不在α中自由出现.
证明 证法同（21），（22）和（23）.
（23）和（24）分别是存在量词对合取的左、右移置律.虽然（20）成立，但其中的→不能换成↔，所以对于存在量词来说，合取分配律不成立.
（25）
∀x（α∨β）→∀xα∨β，x不在β中自由出现.
证明
（26）
∀xα∨β→∀x（α∨β），x不在β中自由出现.
证明
（27）
∀x（α∨β）↔∀xα∨β，x不在β中自由出现.
证明 由（25）和（26）可得.
（28）
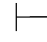∀x（α∨β）↔α∨∀xβ，x不在β中自由出现.
证明 证法同（25），（26）和（27）.
（29）
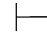∀xα∨∀xβ→∀x（α∨β）.
证明
（27）和（28）分别是全称量词对析取的左、右移置律.虽然（29）成立，但其中的→不能换成↔，所以对于全称量词来说，析取分配律不成立.
（30）
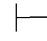∃x（α∨β）→∃xα∨∃xβ.
证明
（31）
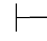∃xα∨∃xβ→∃x（α∨β）.
证明
（32）
∃x（α∨β）↔∃xα∨∃xβ.
证明 由（30）和（31）可得.(https://www.daowen.com)
（33）
∃x（α∨β）→∃xα∨β，x不在β中自由出现.
证明
（34）
∃xα∨β→∃x（α∨β），x不在β中自由出现.
证明
（35）
∃x（α∨β）↔∃xα∨β，x不在β中自由出现.
证明 由（33）和（34）可得.
（36）
∃x（α∨β）↔α∨∃xβ，x不在α中自由出现.
证明 证法同（33），（34）和（35）.
（35）和（36）分别是存在量词对于析取的左、右移置律.（32）是存在量词对于析取的分配律.
（37）
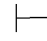∀x⇁α→⇁∃xα.
证明
（38）
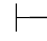⇁∃xα→∀x⇁α.
证明
（39）
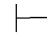∀x⇁α↔⇁∃xα.
证明 由（37）和（38）可得.
（40）
∃x⇁α→⇁∀xα.
证明
（41）
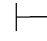⇁∀xα→∃x⇁α.
证明
（42）
⇁∀xα↔∃x⇁α.
证明 由（40）和（41）可得.
（43）
∀xα→⇁∃x⇁α.
证明
（44）
⇁∃x⇁α→∀xα.
证明
（45）
∀xα↔⇁∃x⇁α.
证明 由（43）和（44）可得.
（46）
∃xα→⇁∀x⇁α.
证明
（47）
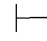⇁∀x⇁α→∃xα.
证明
（48）
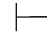∃xα↔⇁∀x⇁α.
证明 由（46）和（47）可得.
（49）
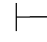∀x（α→β）→（∀xα→∀xβ）.
证明
（50）
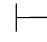∀x（α→β）→（∃xα→∃xβ）.
证明
（51）
∀x（α→β）→（α→∀xβ），x不在α中自由出现.
证明
（52）
（α→∀xβ）→∀x（α→β），x不在α中自由出现.
证明
（53）
∀x（α→β）↔（α→∀xβ），x不在α中自由出现.
证明 由（51）和（52）可得.
（54）
∃x（α→β）→（α→∃xβ），x不在α中自由出现.
证明
（55）
（α→∃xβ）→∃x（α→β），x不在α中自由出现.
证明
（56）
∃x（α→β）↔（α→∃xβ），x不在α中自由出现.
证明 由（54）和（55）可得.
（57）
（∀xα→β）→∃x（α→β），x不在β中自由出现.
证明
（59）
（∀xα→β）↔∃x（α→β），x不在β中自由出现.
证明 由（57）和（58）可得.
（60）
∀x（α→β）→（∃xα→β），x不在β中自由出现.
证明
（61）
（∃xα→β）→∀x（α→β），x不在β中自由出现.
证明
（62）
∀x（α→β）↔（∃xα→β），x不在β中自由出现.
证明 由（60）和（61）可得.
（49）～（62）刻画了量词与蕴涵之间的关系.其中，（53）和（56）是量词对于蕴涵的移置律.（59）和（62）叫做量词转换律，它们把全称量词转换为存在量词，把存在量词转换为全称量词.（49）中的→不能换成↔，即全称量词对蕴涵的分配律不成立.
（63）
∀x（α→β）→（∀x（β→γ）→∀x（α→γ））.
证明
（64）
∀x（α↔β）→（∀xα↔∀xβ）.
证明
（65）
∀x（α↔β）→（∃xα↔∃xβ）.
证明
（66）
∀x（α↔β）→（∀x（β↔γ）→∀x（α↔γ））.
证明
（64）～（66）刻画了量词与等值之间的关系.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
