现在，我们在第三章第四节命题逻辑的自然推理系统FPC的基础上，建立狭谓词逻辑的自然推理系统FQC.并在第六章中证明：狭谓词逻辑的自然推理系统FQC与公理系统QC是等价的.即：一个公式若在FQC中是可证的，当且仅当它在QC中也是可证的.

FQC系统的规则分为三类：结构规则、联结词规则和量词规则.由于前两类规则从形式上看与FPC系统的推理规则相同，所以下面仅给出关于量词的规则.

关于量词的规则如下：

（1）∀+：从α（y/x）可以推出∀xα.这里y既不在∀xα中自由出现，也不在α（y/x）所依赖的假设中自由出现.y被称为关键变项.

（2）∀-：从（∀x）α可推出α（t/x）.

（3）∃+：从α（t/x）可推出∃xα.

（4）∃-：从∃xα和α（y/x）→β可推出β.这里y也被称为关键变项.它既不在∃xα和β中自由出现，也不在α（y/x）→β所依赖的假设中自由出现.

这些规则的图示如图5-1所示。

图5-1

FQC的一个证明就是依上述三类规则构造出来的一个有穷公式序列.另外，第三章第四节的其他概念，也可毫不费力地推广到FQC系统中.下面是对量词规则所作的一些说明.

∀+ 规则叫做全称量词引入规则，它可以表示成为：若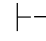α（y/x），则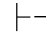∀xα.这里y是关键变项.在使用这个规则时，一定要注意对关键变项所附加的限制条件.规则要求“y也不在α（y/x）所依赖的假设中自由出现”是指，y不在α（y/x）所属子证明利用Hyp规则引入的公式中自由出现，也不在该子证明所从属的子证明，所从属的子证明的子证明等等中，利用Hyp规则引入的公式中自由出现.但是，当x在α中有自由出现而α（y/x）本身又是Hyp规则引入时，就不能直接引用∀+规则而得到∀xα.

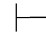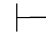∀-规则叫做全称量词消去规则.它可以表示为：若∀xα，则α（t/x）.它反映演绎推理中这样的规则：如果已经断定某个个体域中的一切个体都有某个性质，那么任取该个体域中的一个个体，就可以推知这个个体也具有那个性质.

∃+规则叫做存在量词引入规则.它可以表示为：若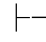α（t/x），则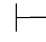∃xα.它反映演绎推理中这样的规则：如果已经断定某个个体域中有个体具有某个性质，那么就可以推知在该个体域中至少有一个个体具有这一性质.

∃-规则叫做存在量词消去规则.它可以表示为：若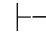α（y/x）→β并且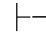∃xα，则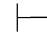β.这里的y是关键变项.它反映演绎推理中的这样的规则：任取个体域中一个个体a，从这个个体有某个性质能推出某个命题，那么个体域中至少有一个个体具有这一性质，也能推出这个命题.因此，当我们想要从给定前提∃xα推出β时，我们不必直接从∃xα出发来进行推导，可以从α（y/x）出发，只要能从α（y/x）推出β，也就证明了从前提∃xα能推出β.这与∀+规则相类似，在使用这一规则时，一定要注意对关键变项所附加的限制条件.规则中所说“也不在α（y/x）→β所依赖的假设中自由出现”是指，y不在α（y/x）→β所属子证明.该子证明所从属的子证明、所从属的子证明所从属子证明等等中，利用Hyp规则引入的公式中自由出现.

定义 FQC的一个证明就是按上述三类规则构造的一个有穷公式序列.如果一个证明在其论证过程中引进的假设并未都用⇁规则和→+规则消除，则称该证明为假设性证明.否则，称该证明为非假设性证明.当α是某个非假设性证明的最后一步时，则称α为（形式）可证的或称为FQC的定理，记作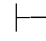α；同时也称该证明为α的一个（形式）证明.(www.daowen.com)

FPC中的可证公式也都是FQC的可证公式.

下面将通过几个例子来说明量词规则的使用.特别是说明，在使用∀+和∃-两个规则时必须注意对关键变项所附加的限制条件，否则会使并非有效的公式成为可证公式.

例3.1

在这个“证明”中，错误地使用了∀+规则，因为α（x/v0）是由Hyp规则引入的，并且由v0在α中自由出现可知x也必在α（x/v0）中自由出现.所以，这个证明是错误的.

例3.2

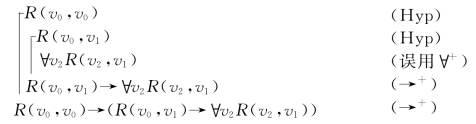
在这个“证明”中，也错误地使用了∀+规则，因为关键变项v0在由Hyp引入的公式R（v0，v0）和R（v0，v1）中自由出现.所以，这个证明是错误的.

例3.3

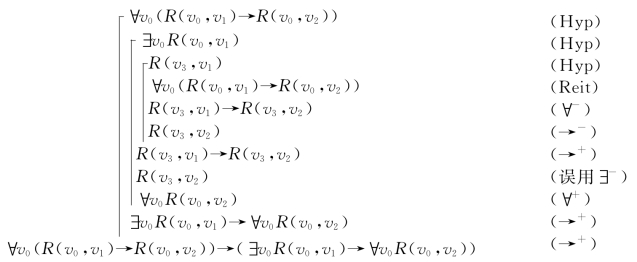
在这个“证明”中，错误地使用了∃-规则，因为关键变项v3在R（v3，v2）中自由出现.

例3.4

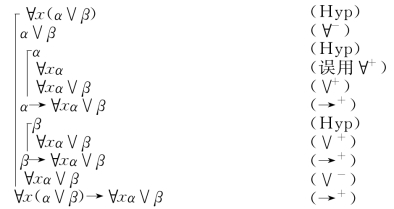
在这个“证明”中，错误地使用了∀+规则，因为α是由Hyp规则引入的，并且不能保证x不在α中自由出现.