谓词演算的公理系统QC建立以后，运用它的公理和推理规则，能生成无穷多条定理.但是，本节中，我们只给出QC系统中常用的，有关量词的一些可证公式及其证明.

由于命题演算系统PC是一阶谓词演算系统QC的一个子系统，因此，PC的定理也都是QC的定理，并且在PC的定理中，用L公式替换后的结果，也都是QC的定理.（不妨设α是PC的定理并且α′是在α中用L公式替换后的结果，那么α在PC中就有一个证明.根据这个证明，我们可以构造一个α′的证明.）特别地，由于FPC系统和PC系统是等价的，所以，在证明中，我们也可以把FPC系统中的定理作为QC系统中已证的定理来使用.

QC系统有下面的定理：

1.∀x（P（x）∨⇁P（x））.

2.∀x P（x）→∃x P（x）.

证明 定理1被称为一阶谓词逻辑的排中律.

关于定理1的证明：

关于定理2的证明：

QC系统有下面的定理：

3.∀x（P（x）∧Q（x））→∀x P（x）∧∀x Q（x）.

4.∀x P（x）∧∀x Q（x）→∀x（P（x）∧Q（x））.

5.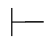∀x（P（x）∧Q（x））↔∀x P（x）∧∀x Q（x）.

7.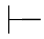∀x（P（x）↔Q（x））→（∀x P（x）↔∀x Q（x））.

8.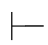∀x P（x）∨∀x Q（x）→∀x（P（x）∨Q（x））.

证明 关于定理3的证明：

关于定理4的证明：

关于定理5的证明：

关于定理6的证明：

关于定理7的证明：

同理可证：

关于定理8的证明：

同理可证：

QC系统有下面的定理：

9.∃x P（x）→⇁∀x⇁P（x）.

10.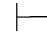⇁∀x⇁P（x）→∃x P（x）.

11.∃x P（x）↔⇁∀x⇁P（x）.(www.daowen.com)

12.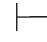∃x⇁P（x）→⇁∀x P（x）.

13.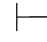⇁∃x⇁P（x）→∀x P（x）.

14.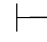⇁∃x P（x）→∀x⇁P（x）.

证明 关于定理9的证明：

关于定理10的证明：

关于定理11的证明：

关于定理12的证明：

同理可证：

关于定理13的证明：

关于定理14的证明：

QC系统有下面的定理：

15.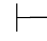∀x（P（x）→Q（x））→（∃x P（x）→∃x Q（x））.

16.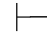∀x（P（x）↔Q（x））→（∃x P（x）↔∃x Q（x））.

证明 关于定理15的证明：

关于定理16的证明：

QC系统有下面的定理：

17.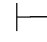∀x∀y R（x，y）↔∀y∀x R（x，y）.

18.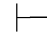∃x∀y R（x，y）→∀y∃x R（x，y）.

证明 关于定理17的证明：

同理可证：

关于定理18的证明：

由此可见，用逻辑系统证明一些公式，不是一件十分容易的事情.也就是说，机械地证明一个定理并不像有些人想象的那么容易.证明的效率与演绎系统和算法的设计都有关系.王浩1958年设计出了一个具有相当高效率的命题演绎系统，他的结果引起了人们的广泛注意（见文献[20]）.但是，引入量词后，证明依旧很困难.

我们将在第六章的第四节中证明：谓词演算系统QC能够推出一阶公式中的所有永真的公式.这样一来，似乎QC的功能非常强了.但是，它的本事也就到此为止.在实际应用中，仅仅推演出永真公式是远远不够的.任何有意义的知识推理系统都要和非永真公式打交道，它的谓词都被指派以某种解释，即语义.在这些系统中的公式，一般都不是永真的.因此，我们应该使用含有语义的演绎系统.不过，现在讨论的这个语法演绎系统依然是一切语义演绎系统的共同基础，仍具有重要的意义.