1.选择适当的符号，把下列语句翻译成一阶语言的语句.

（1）凡事物都是发展变化的.

（2）凡有理数都等于一个分数.

（3）凡实数均能比较大小.

（4）有的事物是有新陈代谢的.

（5）有的自然数是素数.

（6）所有参观者欣赏每一件展品.

（7）所有参观者欣赏一些展品.

（8）有的参观者欣赏每一件展品.

（9）有些参观者欣赏一些展品.

（10）人人都要尊重教师.

（11）并不是每个班的学生都喜欢这门课.

（12）有些学生喜欢下棋好的老师.

（13）张三打败了所有的对手.

（14）所有对手都打败了张三.

2.用自然语言描述下面的一阶公式：

（1）∃v1∀v2（⇁R（N1，N2））；

（2）∀v1∃v2∀v3（R（v2，v3）↔∀v4（R（v3，v4）→R（v1，v4））；

（3）∀v1∃v2∀v3（R（v2，v3）↔∃v4（R（v1，v4）∧R（v4，v3））.

这里的R（x，y）表示y∈x.

3.判断以下符号序列是否一阶公式：

（1）∀x（P（x）∧Q（x））；

（2）∃x R（x，y）∨P；

（3）P（x）→Q（x，y）；(www.daowen.com)

（4）∀x∀x（P（x）∨Q（x））；

（5）∀x⇁（P（x）∧∃y（Q（z）∧R（x，z）））；

（6）∃x（P（x）∧⇁∃y（Q（y）∧R（x，y）））；

（7）P（c）∨∀x P（x）∧Q（w）；

（8）∃x∃y（A（x）∧B（y））.

4.指出下列公式中量词的辖域（即量词的约束范围），指明哪些个体变项是约束出现，哪些是自由出现.

（1）R（x，y）→R（y，x）∧∀y Q（y）；

（2）∀x（P（x）→∃y（R（x，y）∧Q（y）））；

（3）∃x（P（x）→Q（x））→（P（y）→Q（y））；

（4）∀y（R（x，y）∧Q（y））∨∀x P（x）；

（5）∀x∃y R（x，y）→∃y R（z，y）；

（6）∃x P（x）∨∃x R（x，y）→P（y）∨∀x P（x，y）；

（7）∃x∀y R（y，x，z）→∃zR（y，x，z）；

（8）∀x∃y R（x，y）∧∃zR（z，y，x）.

5.求上题中各公式α的sub和free.

6.试用∀和⇁定义∃，试用∃和⇁定义∀.

7.给定符号集S，对于AS中任意符号序列X，规定X的权数w（X）如下：

w（（）=w（））=w（，）=w（⇁）=w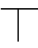（）=w（⊥）=0，

w（x）=w（c）=-1，

w（∨）=w（∧）=w（→）=w（↔）=w（∀）=w（∃）=1，

w（Rn）=n-1（这里Rn是X中的一个n元关系符号），

w（X）=X中所含符号的权的总和.

施归纳于公式的结构，证明任一公式的权等于-1.但是，它的真始段的权都大于等于0.（注：设X，Y，Z都是符号序列，若X=YZ，则称Y是X的一个始段；若Z非空，则称Y是X的真始段.）