定义1.6 设A是一张字母表，由A中的符号组成的有穷序列叫做A上的符号串，简称A上的串.A上的全部符号串的集合记成E（A）.

定义1.7 在一个符号串中出现的符号的个数（同一符号的重复出现按重复的次数计算），称为该符号串的长度.空符号串，称为空串.它的长度为0.由单独一个符号的一次出现组成的符号串，其长度为1.

一个拼音语言，当它的字母表给定以后，人们就可以随意地对字母表中的字母进行排列，这样随意排列出来的符号序列，并不一定都有意义.如：like，model，wuv，bxy等都是英语字母表上的符号串，而like和model有意义，wuv和bxy无意义.又如：令字母表A={0，1，2，…，9，+}，那么1+2和9+3等等所有有意义的算式都是A上的符号串，而且还有许多无意义的符号串，如0+，++9等.

于是，我们需要规定一些拼音规则，使得用这些规则排列出来的符号串有意义，即表示字或者表示一个有意义的语句.对于一阶语言L来说也是如此.我们将规定一些规则，使得按我们的规则所形成的符号序列有意义，否则就无意义.并称这样的符号序列是由S确定的一阶语言LS的项或公式.

定义1.8 LS的形成规则：

甲：个体变项和S中的个体常项统称为S—项；

乙：如果t0，t1，…，tn-1都是S项，而Rn是S中的任一n元谓词符号，那么Rn（t0，t1，…，tn-1）是一个S—公式；

丙：如果α是S—公式，那么⇁α也是；

丁：如果α和β都是S—公式，那么（α∨β）也是；

戊：如果α是一个S—公式，而x是一个个体变项，那么∀xα和∃xα都是S—公式；

己：E（AS）中的符号串是S—公式，当且仅当该符号串可由上述规则乙～戊的有穷多次运用而得.

当S在上下文中显然或不重要时，我们也常把S—项和S—公式分别简称为项和公式.S项用t或加下标表示。

当S—公式的全体组成的集合记作WS或LS或W.其中，由规则乙形成的S—公式R（t0，t1，…，tn-1）称为原子公式，按规则丙形成的公式⇁α叫做α的否定式.由规则丁形成的公式（α∨β）称为α和β的析取式，由规则戊形成的公式∀xα和∃xα分别称为α的全称式和存在式，这里的x为量化变项，而符号串xα为初始符号∀和∃的辖域.

为经济起见，我们只给出了两个二元联结词。因此，现在我们谈论或使用符号∧或→等都没有意义.为了使用方便，现在我们将通过定义引入其他联结词.

定义1.9

定义甲：（α∧β）被定义为⇁（⇁α∨⇁β）.

定义乙：（α→β）被定义为（⇁α∨β）.

定义丙：（α↔β）被定义为（（α→β）∧（β→α））.

现在，我们可以将等式左端的式子看成等式右端式子的缩写.

下面是S—公式的一些例子.

例1.4 将命题“2是偶数”和“郑州在开封和洛阳之间”写成S—公式.

解 令P（v）表示“v是偶数”，这里P是一个一元谓词，即性质，v是个体变项；令Q（v0，v1，v2）表示“v0在v1和v2之间”，这里Q是一个三元谓词（或关系词），v0，v1和v2是个体变项，则P（2）和Q（郑州，开封，洛阳）分别表示“2是偶数”和“郑州在开封和洛阳之间”，这里“2”、“郑州”、“开封”和“洛阳”都是个体常项.

这里值得注意的是：命题“2是偶数”，在命题逻辑中原本是一个简单命题，可记作p.但是，在狭谓词逻辑中，我们又对它作了进一步分析.把它表示成原子公式P（2）.因此，所有的简单命题都可以表示成原子公式.由此可得：命题公式集W0是一阶公式集W的一个子集.即：W0⊆W.

例1.5 将命题“对任一自然数，都有一个比它大的素数”表示成一阶公式.

解 令∀x表示：“任一x”，∃y表示：“有一y”，P1（x）表示：“x是自然数”，Q1（y）表示：“y是素数”，R（x，y）表示“y大于x”，原命题可以表示为以下S—公式：

∀x（P1（x）→∃y（Q1（y）∧R（x，y）））.

例1.6 把论断：“世上决没有无缘无故的爱，也没有无缘无故的恨”表达成一阶公式的形式.

解 最简单的表示方法是用一个单个的命题变项来表示，如：

p

从推理的角度看，我们还应该把这个论断的表示形式再细分.在这个意义上，上述命题起码可以再细分为：

（1）式已被分解为两个命题.

（2）式把否定词分析了出来.

（3）式把存在量词分析了出来.

（4）式把爱和恨的概念分析了出来.

（5）式把缘故的否定词分析了出来.

（6）式又把“A是B的原因”这个概念中的A和B分解了出来.

例1.7 令S={R}，R是一个二元关系符号，下面的三个符号串都是S—公式：

（1）∀v0 R（v0，v0）；

（2）∀v0∀v1（R（v0，v1）→R（v1，v0））；

（3）∀v0∀v1∀v2（R（v0，v1）∧R（v1，v2）→R（v0，v2））.

解 （1）说明每一个体与其自身有R关系.也就是说，R具有自返性；（2）说明如果一个个体与另一个体有R关系，则后一个体也与前一个体有R关系.也就是说，R具有对称性；（3）说明如果个体v0与个体v1有R关系而个体v1与个体v2也有R关系，则个体v0与个体v2也有R关系.也就是说，R具有传递性.因此，这三个公式刻画了第一章中等价关系理论中的三条公理.即：R是一个等价关系.这里的R（x，y）通常记成x Ry.

例1.8 令S={R，=}，R和=都是二元关系符号，下面的符号串是S—公式：

（1）∀v0 R（v0，v0）；

（2）∀v0∀v1（R（v0，v1）∧R（v1，v0）→（v0=v1））；(www.daowen.com)

（3）∀v0∀v1∀v2（R（v0，v1）∧R（v1，v2）→R（v0，v2））.

解 （1）说明R是自返的；（2）说明R是反对称的；（3）说明R是传递的.因此，这三个公式恰好刻画了第一章中偏序关系理论中的三条公理，即R是一个偏序关系.这里的R（x，y）通常也记成x Ry.

一阶语言LS是我们的研究对象.在研究它们时，我们要使用汉语和一些数学符号来进行讨论.因此，前者是对象语言，后者是元语言.这一点我们必须注意区分.

类似于第三章第二节的定理，要想证明LS中每个公式都具有某个性质φ，我们只要证明下面的定理.

定理 LS中的一切S—公式均具有性质φ，如果满足：

（1）每个形如R（t0，t1，…，tn-1）的S—公式有性质φ；

（2）如果S—公式α有性质φ，则⇁α亦然；

（3）如果S—公式α和β都有性质φ，则（α∨β）也有性质φ；

（4）如果S—公式α有性质φ并且x是一个个体变项，则∀xα和∃xα也都有性质φ.

用这种方法证明关于公式的一些结论时，我们说施归纳于公式的结构.这种证明的思想是归纳法的思想.同样，如果在LS上定义一个概念，如映射，也可施归纳于公式的结构，只要完成下面的四步即可：

第一步，对各个原子公式指派真值；

第二步，如果已经对α指派了真值，然后确定⇁α的真值；

第三步，如果已经对α和β指定了真值，然后确定（α∨β）的真值；

第四步：如果对α指定了真值，然后确定∀xα和∃xα的真值.这种定义方式也称作公式上的归纳定义.作为这种证明方法的运用，我们来完成下面引理1.1的证明.

引理1.1 每个S—公式所含的左括号的个数等于其中所含右括号的个数.

证明 α有性质φ，当且仅当，α中所含左括号的个数等于其中所含右括号的个数.

施归纳于公式的结构.

（1）每个形如R（t0，t1，…，tn-1）的S—公式中，只有一个左括号和一个右括号.因此，结论成立.

（2）设结论对S—公式α成立，即α中左括号的个数等于右括号的个数.根据定义1.8丙可知，⇁α所含括号数与α所含括号数完全相同，因此结论对⇁α也成立.

（3）设结论对S—公式α和β都成立.根据定义1.8丁可知，S—公式（α∨β）中所含左括号数是α中的左括号个数加上β中的左括号个数再加1，而（α∨β）中所含右括号数是α中的右括号个数加上β中的右括号个数再加1.由假设可知：α中的左括号数等于α中的右括号数，β中的左括号数等于β中的右括号数.因此，结论对S—公式（α∨β）成立.

（4）设结论对S—公式α成立.由于x是个体变项.根据定义1.8戊可知，S—公式∀xα和∃xα中所含左括号数都是α中左括号数，它们所含的右括号数都是α中右括号数，由假设可知：α中所含左括号数等于α中所含右括号数.因此，结论对S—公式∀xα和∃xα成立.

定义1.10 设S是任意的符号集，对于E（AS）中的任一个符号串s，我们规定s的权，记作w（s），如下：

w（（）=w（））=（，）=w（⇁）=w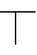（）=w（⊥）=0，

w（x）=w（c）=-1，

w（∨）=w（∀）=w（∃）=1，

w（R）=n-1（这里R是S中的一个n元关系符号），

w（s）=s中所含符号的权的总和.

如：w（R（t0，t1，…，tn-1））=（n-1）+n·（-1）=-1.

定义1.11 设s是一个符号串，如果s可以写成s0s1，那么称s0为s的始段，并称s1为s的终段.当s0或s1不是空串时，称s0是s的真始段，s1是s的真终段.

引理1.2 任一公式的权是-1.但是，它的真始段的权数都大于等于0.

证明 证明留给读者去做.

由引理1.2可知，对任意的公式α和α′，α不能是α′的一个真始段.利用这一点，我们可以证明每一个公式有且仅有下列各种形式之一：R（t0，t1，…，tn-1），⇁α，（α∨β），∀xα和∃xα.

定义1.12 对于任一公式α，α的全体子公式sub（α）定义如下：

（1）sub（R（t0，t1，…，tn-1））={R（t0，t1，…，tn-1）}；

（2）sub（⇁α）={⇁α}∪sub（α）；

（3）sub（（α∨β））={α∨β}∪sub（α）∪sub（β）；

（4）sub（∀xα）={∀xα}∪sub（α），

sub（∃xα）={∃xα}∪sub（α）.

由此可得：

sub（（α∧β））={α∧β}∪sub（α）∪sub（β），

sub（（α→β））={α→β}∪sub（α）∪sub（β），

sub（（α↔β））={α↔β}∪sub（α）∪sub（β）.