在命题逻辑中，起本质作用的是联结词.我们已在第三章中确定了常用联结词的意义和使用规则.在命题逻辑中，主要研究的是复合命题的逻辑性质和推理关系，复合命题是由简单命题和联结词组成的，它的真假由所含简单命题的真假和所含联结词的意义所确定.简单命题是命题逻辑的基本单位.在命题逻辑中，我们并不分析这些基本单位又具有怎样的逻辑特征和结构.因此，使得有些命题之间正确的推理关系（如：传统的三段论原则）在命题逻辑中得不到反映.例如：

所有金属都是导电体；

铁是金属；

所以，铁是导电体.

这是一个正确的推理.但是，在命题逻辑里，它的前提和结论只能处理成不同的简单命题，它的推理形式只能是：

p，

q，

所以，r.(www.daowen.com)

即：{p，q}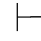0 r.显然，这不是命题逻辑中正确的推理形式.但是，这个推理是正确的，它的正确性并不能在命题逻辑中表现出来.造成这一现象的原因就在于，这个推理的正确性依赖于前提和结论中所含命题的内部结构.因此，要表现这类推理的正确性，就必须建立新系统.在新系统中，首先要涉及简单命题的内部结构，即对简单命题作进一步分析.只有这样，才能揭示前提和结论在形式结构方面的联系，也才能认识这类推理的形式和规律.

本章讨论的狭谓词逻辑也是数理逻辑的基础部分.狭谓词逻辑将包含命题逻辑作为一个子系统.因此，在狭谓词逻辑中，前面关于复合命题的逻辑性质及其推理关系的讨论仍然成立.本章将对命题逻辑的基本单位——简单命题继续分解，分解出个体词、谓词（即关系词）和量词，从而揭示简单命题的形式结构，研究它们的逻辑性质和规律，使之能更深入、更广泛地表现实际推理过程.但这里的重点是研究量词的逻辑性质和关于它们的推理规律.但是，在狭谓词逻辑中，量词只允许修饰个体变项，不允许修饰命题变项和谓词.也就是说，在狭谓词逻辑中，我们只研究如下形式的公式：

∀x Q（x），

不研究如下形式的公式：

∀p（p→p），

∀Q∀x（P（x）∧⇁P（x））.

这里p是命题变项，∀是全称量词，x是个体变项，P是一元谓词.所以，称这样的谓词逻辑为狭谓词逻辑.