本节我们将采用算术解释方法给出PC系统公理的独立性证明.

定义5.1 一个公式集Φ是独立的，如果Φ中的每一个公式α都不能根据给定的推演规则从Φ中用其他公式推演出来.

这里需要注意：独立性就是不可推演性，并且独立性总是相对于给定的推理规则而言的.应用某些推理规则，不能推出公式α，应用另一些推理规则就可能推演出公式α.

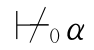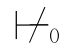或者说，公式α是独立于公式集Φ的，如果α和⇁α都不是Φ的推论，即：Φ并且Φ⇁α.由第四章定理2.2可得：Φ，α相容并且Φ，⇁α也相容.于是，就可以分别将Φ，α和Φ，⇁α扩充成极大相容的公式集，而每个极大相容的公式集都可满足（可参考第六章的第四节的相关内容）.因此，Φ，α可满足并且Φ，⇁α也可满足.于是，存在一个真值赋值σ使得σ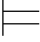Φ，α并且存在一个真值赋值σ′使得σ′Φ，⇁α.对公理A1，A2，A3，A4而言，因为A1，A2，A3，A4都是重言式，所以对任意的真值赋值σ，都有σ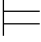A1，A2，A3，A4，即：A1，A2，A3，A4是可满足的.因此，要证明公理A1，A2，A3，A4之间的相互独立性，现在只需考虑下面四种情况：

1.令α=A1，Φ1={A2，A3，A4}.现在只需构造一个赋值σ1使得σ1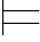A2，A3，A4并且

2.令α=A2，Φ2={A1，A3，A4}.现在只需构造一个赋值σ2使得σ2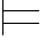A1，A3，A4并且

3.令α=A3，Φ3={A1，A2，A4}.现在只需构造一个赋值σ3使得σ3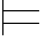A1，A2，A4并且

4.令α=A4，Φ4={A1，A2，A3}.现在只需构造一个赋值σ4使得σ4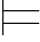A1，A2，A3并且

以下是命题演算PC系统的诸公理的独立性证明.

公理A1的独立性是指：命题演算PC系统的公理A1不能从PC系统的其余公理A2，A3和A4应用推理规则MP推演出来.

1.公理A1的独立性证明

算术解释：

（1）命题变项p，q，r，s，p1，…可有三个值0，1和2.

（2）初始联结词的数值表如下：

（3）联结词→的数值表如下：

公理A1的数值表为：

公理A2的数值表为：

公理A3的数值表为：

公理A4的数值表为：

从以上数值表可以看出：公理A2，A3和A4的数值常为0，但公理A1的数值不常为0.从给定的→的数值表可以看出，当α和α→β的数值皆为0时，β的值也是0.所以，如果α和α→β的值常为0，则β的值也常为0.因此，应用分离规则从公理A2，A3和A4只能得到其值常为0的公式，故公理A1不能从其他公理推出.即：公理A1独立于公理A2，A3和A4.亦即：命题演算PC的公理A1不能从公理A2，A3和A4应用推理规则MP推出.

2.公理A2的独立性证明

算术解释：

（1）命题变项p，q，r，s，p1，…可有三个值0，1和2.

（2）初始联结词的数值表如下：

（3）联结词→的数值表如下：

公理A1的数值表为：

公理A2的数值表为：(www.daowen.com)

公理A3的数值表为：

公理A4的数值表为：

由此可得：公理A2独立于公理A1、A3和A4.

3.公理A3的独立性证明

算术解释：

（1）命题变项p，q，r，s，p1，…可有三个值0，1和2.

（2）初始联结词的数值表如下：

（3）联结词→的数值表如下：

公理A1的数值表为：

公理A2的数值表为：

公理A3的数值表为：

公理A4的数值表为：

由此可得：公理A3独立于公理A1、A2和A4.

4.公理A4的独立性证明

算术解释：

（1）命题变项p，q，r，s，p1，…可取三个值0，1和2.

（2）初始联结词的数值表如下：

（3）联结词→的数值表如下：

公理A1的数值表为：

公理A2的数值表为：

公理A3的数值表为：

公理A4的数值表为：

根据算术解释，公理A1，A2和A3的值常为0或2，推理规则也传递“等于0或2”这一性质，但公理A4并不常“等于0或2”.当α取值1、β取值2、γ取值0时，公理A4的值为1.所以，公理A4独立于公理A1，A2和A3.

例5.2 （独立性）证明下面的语句独立于文件Buridan's Sentences中的语句，即：这个语句和它的否定都不是那些语句的推论.

∃x∃y（x≠y∧Tet（x）∧Tet（y）∧Medium（x）∧Medium（y））

要建立两个世界才能完成这个工作.其中在一个世界中使这个语句为假，在另一个世界中使这个语句为真.但是在这两个世界中都使所有的Buridan's Sentences中的语句为真.