可靠性是逻辑系统的一个重要性质，它表明逻辑系统正确地反映了演绎推理的规律，作为推理工具是可靠的.当把逻辑系统中的推理规则和逻辑规律应用于其他理论作推理和证明时，不会由所用的逻辑工具而产生矛盾.

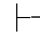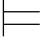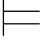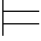在本节里，我们将首先证明公理系统PC的可靠性，然后证明自然推理系统FPC的可靠性.也就是要证明下面的断言：在PC（或FPC）系统中，如果Φ0α，那么Φ0α.即：如果α是从Φ可演绎的，那么α是Φ的重言后承.亦即：对任意的真值赋值σ，如果σΦ，则σα.特别地，如果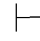0α，则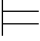0α.即：如果一个公式α在系统中是可证的，则α是常真的.

定理3.1 （PC系统可靠性定理） （1）如果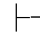Φ0α，则Φ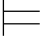0α.（2）如果0α，则0α.

证明 （1）的证明：因为Φ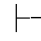0α，所以令φ0，φ1，…，φn 是α的一个从Φ而来的演绎，并且φn=α.下面施归纳于k=0，1，…，n，证明Φ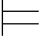0φk （当k=n时，就有Φ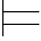0α）.

当k=0时，如果φk 是一个命题公理，由第三章习题3.3.3的1知，φk 是重言式.于是，它为每一真值赋值所满足.故它是任意公式集的重言后承.即：若0φk，则Φ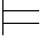0φk.如果φk ∈Φ，则显然当Φ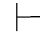0φk 时，有Φ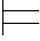0φk.

假设对所有的i＜k，当Φ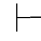0φi 时，有Φ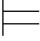0φi.

最后证明：对任意的k，有Φ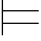0φk.

①如果φk 是公理，那么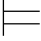0φk，故Φ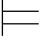0φk ；如果φk ∈Φ，那么Φ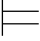0φk.

②如果φk 是由φi 和φj 运用MP规则而得，并且φj=φi →φk，1≤i，j＜k，那么由归纳假设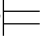：Φ0φi，Φ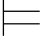φj，即有：Φ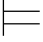0φi →φk，Φ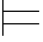0φi.由第三章第六节定理6.3得：{φi，φi →φk }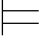0φk.因此显然有：Φ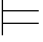0φk.

（2）是（1）的特殊情况，即Φ=∅的情况.

对可靠性而言，如果{φ0，φ1，…，φn }⊆Φ，那么由{φ0，φ1，…，φn }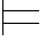0α可得Φ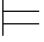0α.再根据第三章第六节定理6.1，即：

所以，“如果Φ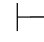0α，那么Φ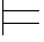0α”的证明也可以归结为证明：如果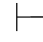0α，那么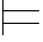0α.即对前面的（1）的证明做适当的简化.

由于PC系统与FPC系统是等价的，那么我们现在就可以下结论：对FPC系统而言，可靠性定理成立.不过，下面将重述并证明在FPC系统中的可靠性定理.

定理3.2 （FPC系统的可靠性定理） （1）如果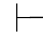0α，那么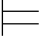0α；（2）如果Φ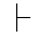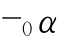，那么Φ0α.

证明 先证（1），然后利用（1）证明（2）.

因为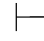0α，那么存在一个证明，这个证明的长度是有限的，即：在这个证明中的公式只有有穷多个，按从前到后的顺序，不妨记为：φ0，φ1，…，φi，…，φn，而φn=α.我们将施归纳于i证明：

对一切真值赋值σ，如果σ满足φi所依赖的由Hyp规则引入的公式，则σ满足φi. （*）如果（*）式成立，当i=n时，有σ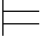φn （即：σ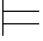α）.由于φn 不依赖于由Hyp规则引入的公式，因此，α为任何真值赋值所满足.所以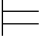，0φn.即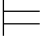：0α，从而证毕.

1.当i=0时，假设真值赋值σ满足φ0 所依赖的由Hyp规则引入的公式.由于此时φ 0只能由Hyp引入，故φ 0依赖于自身，所以（*）式成立.

2.假设（*）式对φ0，φ1，…，φj （j＜n）已经成立.现在只需证明（*）式对φj+1也成立即可.(www.daowen.com)

设真值赋值σ满足φj+1所依赖的由Hyp引入的公式.根据得到φj+1的规则不同，我们将考虑下面12种情况.

①如果φj+1是利用Hyp规则而得到的公式，由1的结论显然成立.

②如果φj +1是利用Rep规则而得到的公式，那么在φj +1所属的子证明中必有某个φm（m≤j），使得φj+1=φm.由于φ m和φj 同属于一个子证明，因此φ m所依赖的由Hyp规则引入的公式跟φj +1所依赖的相同.根据归纳假设有：σ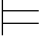φm，于是σ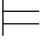φj+1.

③如果φj+1是利用Reit规则而得到的公式，那么必定有某个φm（m≤j），使得φj+1=φm，并且φj+1所从属的子证明必定从属于φ m所属的子证明.因此，φm所依赖的、由Hyp规则引入的公式也是φj+1所依赖的.根据归纳假设有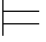：σφm，即σ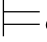φj+1.

④如果φj+1是利用→+规则而得到的公式，那么必有某个φm（m≤j）是由Hyp规则引入的，并且φ j是由φ m开始的子证明的最后一步.因此，我们有φj+1=φm→φj.而φ j所依赖的、由Hyp规则引入的公式，就是φ m再加上φ j+1所依赖的那些公式.如果σ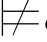 φj+1，那么σ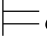φ m并且σ 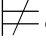φj.但此时σ将满足φ j所依赖的所有公式，根据归纳假设得：σ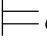φj，这是一个矛盾.所以，σ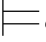φj+1.

⑤如果φ j+1是利用→-规则而得到的公式，那么存在m1，m2≤j使得φm2=（φm1→φj+1），这里φm1，φ m2和φj+1都属于一个子证明.因此，φm1，φ m2所依赖的、由Hyp规则引入的公式跟φ j+1所依赖的相同.根据归纳假设有：σ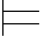φ m1和σ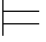φm2.如果σ 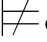φj+1，那么由σ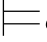φ m2必有σ 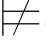φm1，这是一个矛盾.所以，σ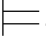φj+1.

⑥如果φ j+1是利用∧+规则而得到的公式，那么在φ j+1所属的子证明中必有φm1，φm2（m1，m2≤j），使得φj+1=（φm1∧φm2），其中φ m1和φ m2所依赖的、由Hyp规则引入的公式都与φj+1所依赖的相同.根据归纳假设得：σ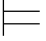φ m1和σ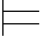φm2，所以σ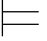（φm1∧φm2），即σ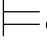φj+1.

⑦如果φ j+1是利用∧-规则而得到的公式，那么必有某个公式φ和自然数m（m≤j），使得φm=（φ∧φj+1）或者φm=（φj+1∧φ），这里φ m和φ j+1同在一个子证明中.因此，φ m所依赖的、由Hyp规则引入的公式都与φj+1所依赖的相同.根据归纳假设得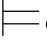：σφm，即σ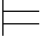（φ∧φj+1）或σ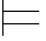（φj+1∧φ），故：σ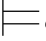φj+1.

⑧如果φ j+1是利用∨+规则而得到的公式，那么必有某个公式φ和某个自然数m（m≤j），使得φj+1=（φm∨φ）或者φj+1=（φ∨φm），这里φ m和φj+1同在一个子证明中.因此，φm所依赖的、由Hyp规则引入的公式都与φ j+1所依赖的相同.根据归纳假设有：σ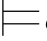φm，因此，σ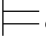φ∨φ m和σ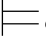φm∨φ，所以，σ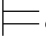φj+1.

⑨如果φ j+1是利用∨-规则而得到的公式，那么一定存在公式ψ1，ψ2和自然数m1，m2和m3（m1，m2，m3≤j），使得φm1=ψ1∨ψ2，φm2=ψ1→φj+1，φm3=ψ2→φj+1；这里的φm1，φm2，φ m3和φ j+1同在一个子证明中.因此，φm1，φ m2和φ m3三者所依赖的、由Hyp规则引入的公式都跟φ j+1所依赖的相同.根据归纳假设有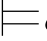：σφm1，σ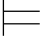φ m2和σ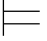φm3.如果σ 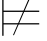φj+1，那么由φm2=ψ1→φj+1和φm3=ψ2→φj+1知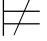，σ ψ1并且σ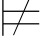 ψ2.因此，σ 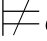ψ1∨ψ2，即：σ 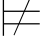φm1.这是一个矛盾，故σ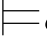φ j+1.

⑩如果φ j+1是用↔+规则而得到的公式，那么一定存在公式φ，ψ和自然数m1和m2（m1，m2≤j），使得φm1=φ→ψ，φm2=ψ→φ，而且φj+1=φ↔ψ；φm1，φm2和φj+1同在一个子证明中.因此φ m1和φ m2所依赖的、由Hyp规则引入的公式都与φ j+1所依赖的相同.根据归纳假设有：σ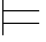φ m1和σ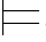φm2.因此，σ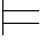（φ→ψ）和σ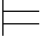（ψ→φ）.即σ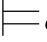φ↔ψ.于是，σ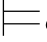φj+1.

⑪如果φ j+1是利用↔-规则而得到的公式，那么存在自然数m1和m2（m1，m2≤j），使得φm1=（φm2↔φj+1）或者φm1=（φj+1↔φm2），而且φm1，φ m2和φ j+1同在一个子证明中.因此，φ m1和φ m2所依赖的、由Hyp规则引入的公式都与φj+1所依赖的相同.根据归纳假设有：σ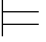φ m1和σ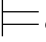φm2.因此，σ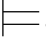φm2.于是，σ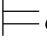φ j+1.

⑫如果φ j+1是利用⇁规则而得到的公式，那么一定存在某个公式ψ和自然数m1，m2和m3（m1，m2，m3≤j），使得φm1=⇁φj+1，φm2=ψ而且φm3=⇁ψ.由于公式φ m1本身是由Hyp规则引入的，而φm2，φ m3所依赖的、由Hyp规则引入的公式就是φ m1再加上φ j+1所依赖的那些公式.如果σ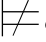 φj+1，那么σ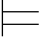⇁φj+1，即：σ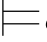φm1.因此，σ满足φ m2和φ m3所依赖的、由Hyp规则引入的公式.根据归纳假设有：σ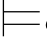φ m2并且σ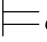φm3，即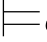：σψ和σ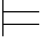⇁ψ，这是不可能的.所以，σ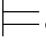φj+1.

至此，我们完成了归纳步骤的证明.根据归纳法知，断言（*）式成立，从而（1）获证.

（2）的证明如下：

设Φ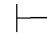0α，则Φ中含有有穷多个公式φ0，φ1，…，φn 满足

由（1）得

因此，满足φ0，φ1，…，φn的任一真值赋值也一定满足α.由于φ0，φ1，…，φn都属于Φ，因此满足Φ的真值赋值也满足φ0，φ1，…，φn，从而满足α.所以，Φ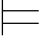0α.