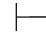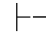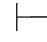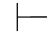定义 令Φ是任一公式集，如果存在一个公式β，使得Φ0β并且Φ0⇁β，那么称公式集Φ是不相容的.否则，称Φ是相容的（即不存在公式β，使得Φ0β并且Φ0⇁β）.

根据以上定义，显然空公式集是相容的.相容的公式集还具有如下一些性质：

性质1（有穷特征） 公式集Φ是相容的，当且仅当Φ的每个有穷子集都相容.

证明 如果Φ是相容的，并且存在Φ的一个有穷子集Φ0不相容，即Φ0⊆Φ.由不相容定义，存在一个公式β，使得Φ0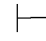0β并且Φ0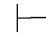0⇁β.由第四章第一节演绎的性质1可得：Φ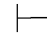0β并且Φ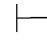0⇁β.此与Φ相容矛盾.故Φ的每个有穷子集都相容.

反之，如果Φ的每个有穷子集都相容并且Φ是不相容的.根据不相容定义，就存在一个公式β，使得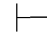Φ0β并且Φ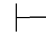0⇁β.由第四章第一节演绎的性质3得：分别有Φ的有穷子集Φ0和Φ1，使得Φ0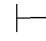0β并且Φ1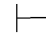0⇁β.由性质1得：Φ0∪Φ1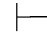0β并且Φ0∪Φ1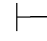0⇁β，这里Φ0∪Φ1仍然是Φ的有穷子集，此与Φ的每个有穷子集都相容矛盾！故：Φ相容.

性质2（基本相容性） 对任意的命题变项p，{p，⇁p}是不相容的.特别地，{⊥}不相容.

性质3（合取保持性） 令Φ是一个相容的公式集，并且α，β是任意的公式，那么下面的结论成立：

（1）如果（α∧β）∈Φ，那么Φ∪{α，β}相容；

（2）如果⇁（α∨β）∈Φ，那么Φ∪{⇁α，⇁β}相容；

（3）如果⇁（α→β）∈Φ，那么Φ∪{α，⇁β}相容.

性质4（析取保持性） 令Φ是一个相容的公式集，并且α，β是任意的公式，那么下面的结论成立：

（1）如果（α∨β）∈Φ，那么Φ∪{α}相容或Φ∪{β}相容；

（2）如果⇁（α∧β）∈Φ，那么Φ∪{⇁α}相容或Φ∪{⇁β}相容；

（3）如果α→β∈Φ，那么Φ∪{⇁α}相容或Φ∪{β}相容.

性质5（否定的保持性） 令Φ是一个相容的公式集，并且α是任意的公式，如果⇁⇁α∈Φ，那么Φ∪{α}相容.

根据本节相容性的定义，很容易得到性质2～5的证明.

关于不相容性，我们有下面的一些结论：

定理2.1 公式集Φ是不相容的，当且仅当对每一公式α，都有Φ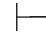0α.

证明 如果Φ是不相容的，那么存在一个公式β，使得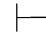Φ0β并且Φ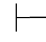0⇁β成立.由第四章第一节演绎的性质6得：对任何公式α，都有Φ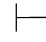0α.

反之，如果对任一公式α，都有Φ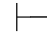0α，那么对某个（实际上，对一切）β，有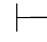Φ0β及Φ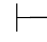0⇁β.故Φ是不相容的.

定理2.2 对任意的公式集Φ和公式α，有：

（1）Φ，⇁α是不相容的，当且仅当Φ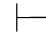0α.

（2）Φ，α是不相容的，当且仅当Φ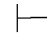0⇁α.

证明 （1）因为Φ，⇁α不相容，由定义可得：Φ，⇁α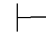0β和Φ，⇁α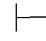0⇁β.再由第四章第一节演绎的性质11得：Φ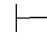0⇁α→β和Φ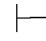0⇁α→⇁β.利用第三章第五节定理5.81，即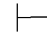：0（⇁α→β）→（⇁α→⇁β）→α.再运用第四章第一节演绎的性质4和性质9可得Φ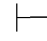0α.反之，如果Φ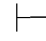0α，因为由第四章第一节演绎的性质1和2可得：Φ，⇁α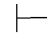0α并且Φ，⇁α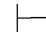0⇁α.故Φ，⇁α不相容.(www.daowen.com)

（2）因为Φ，α不相容，由定理2.1可得：Φ，α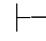0⇁α.由第四章第一节演绎的性质11可得：Φ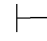0α→⇁α.利用第三章第五节定理5.2和定理5.7，即：

由此可得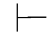：0（α→⇁α）→⇁⇁α→⇁α.由第四章第一节演绎的性质4得：Φ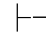0⇁⇁α→⇁α.再用第三章第五节定理5.81和定理5.3，即：于是，由第四章第一节演绎的性质4和9可得：Φ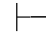0⇁α.反之，因为Φ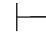0⇁α，并且Φ⊆{Φ，α}，所以由第四章第一节演绎的性质1和2有：Φ，α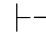0⇁α和Φ，α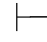0α，故Φ，α不相容.

定理2.3 令Φ是任意的公式集，对任意的公式α，β

（1）如果α→β∈Φ，且Φ，⇁α及Φ，β皆不相容，那么Φ不相容.

（2）如果⇁（α→β）∈Φ，且Φ，α，⇁β不相容，那么Φ不相容.

证明 （1）因为Φ，⇁α不相容，由定理2.2（1）得：Φ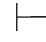0α.又因Φ，β不相容，由定理2.2（2）得：Φ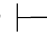0⇁β.由于α→β∈Φ，根据第四章第一节演绎的性质2得：Φ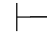0α→β.于是有：Φ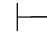0β（演绎的性质9）.故Φ不相容.

（2）因为⇁（α→β）∈Φ，由第四章第一节演绎的性质2得：Φ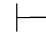0⇁（α→β）.又因为Φ，α，⇁β不相容，根据定理2.2（1）：Φ，α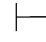0β.再用第四章第一节演绎的性质11得：Φ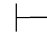0α→β.故Φ不相容.

定理2.4 令Φ是任意的公式集，对任意的公式α，β，

（1）如果α∧β∈Φ，并且Φ，α或Φ，β不相容，那么Φ不相容.

（2）如果⇁（α∧β）∈Φ，并且Φ，⇁α及Φ，⇁β不相容，那么Φ不相容.

证明 （1）因为α∧β∈Φ，由第四章第一节演绎的性质2得：Φ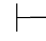0α∧β.于是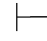Φ0α并且Φ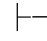0β.又因Φ，α或Φ，β不相容，根据定理2.2（2）得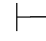：Φ0⇁α或Φ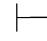0⇁β.故Φ不相容.

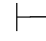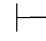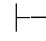（2）因为⇁（α∧β）∈Φ，由第四章第一节演绎的性质2得：Φ0⇁（α∧β）.又因Φ，⇁α及Φ，⇁β不相容，根据定理2.2（1）得：Φ0α且Φ0β，即：Φ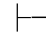0α∧β，故Φ不相容.

定理2.5 令Φ是任意的公式集，对任意的公式α，β，

（1）如果α∨β∈Φ，且Φ，α及Φ，β都不相容，那么Φ不相容.

（2）如果⇁（α∨β）∈Φ，且Φ，⇁α或Φ，⇁β不相容，那么Φ不相容.

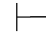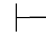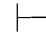证明 （1）因为α∨β∈Φ，由第四章第一节演绎的性质2得：Φ0α∨β.又因为Φ，α及Φ，β都不相容，根据定理2.2（2）得：Φ0⇁α且Φ0⇁β，即：Φ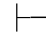0⇁α∧⇁β.由此得：Φ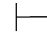0⇁（α∨β），故Φ不相容.

（2）因为⇁（α∨β）∈Φ，由第四章第一节演绎的性质2得：Φ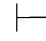0⇁（α∨β）.又因为Φ，⇁α或Φ，⇁β不相容，根据定理2.2（1）得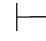：Φ0α或Φ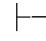0β，由演绎的性质8，得：Φ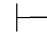0α∨β，故Φ不相容.

定理2.6 令Φ是任意的公式集，对任意的公式α，β，

（1）如果α↔β∈Φ，且Φ，⇁α及Φ，β皆不相容或Φ，α及Φ，⇁β皆不相容，那么Φ不相容.

（2）如果⇁（α↔β）∈Φ，且Φ，⇁α，β及Φ，α，⇁β皆不相容，那么Φ不相容.

（2）因为⇁（α↔β）∈Φ，由第四章第一节演绎的性质2得：Φ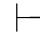0⇁（α↔β）.又因为Φ，⇁α，β及Φ，α，⇁β皆不相容，根据定理2.2（1）和（2）得：Φ，β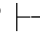0α且Φ，α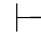0β.再由第四章第一节演绎的性质11得：Φ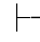0β→α，且Φ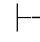0α→β，即：Φ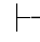0（α↔β），故Φ不相容.