定义 令Φ是一个公式集，φ是一个公式.如果φ是某个假设性证明的最后一步得出的公式，而该假设性证明的所有未曾消除的由Hyp规则所引入的公式都属于Φ，那么称公式φ是从公式集Φ可演绎的.简称φ是从Φ可演绎的.记作Φ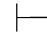0φ.当Φ是空集时，即Φ=∅，记作∅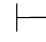0φ，简记为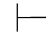0φ，即φ为系统内定理.当Φ只有一个元素时，即Φ={ψ}，记作{ψ}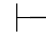0φ，或简记为ψ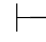0φ，并称φ可从ψ演绎.当公式集是Φ∪{ψ}时，即Φ∪{ψ}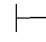0φ，简记作Φ，ψ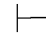0φ.在不引起混淆时，下标0可以省略.

演绎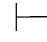0具有下面的一些性质：

性质1 如果Φ和Φ′都是公式集，并且Φ⊆Φ′，而Φ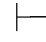0α，那么Φ′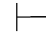0α.

证明 根据可演绎定义，Φ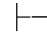0α，即有一个假设性证明，它的最后一个公式是α，而所有未经消除的假设都属于Φ.由于Φ⊆Φ′，所以，所有这些未经消除的假设也都属于Φ′，故Φ′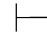0α.

性质2 如果α∈Φ，那么Φ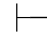0α.

证明 存在仅含一个公式α的假设性证明如下：

-α Hyp

因为α∈Φ，按可演绎定义，有Φ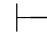0α.

性质3 Φ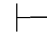0α，当且仅当有一个Φ的有穷子集Φ0，Φ0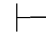0α.

证明 如果Φ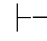0α，那么有一个假设性证明，它以α为最后一步得出的公式，而所有未被消除的假设都属于Φ，这些未被消除的假设的全体就是Φ的一个有穷子集，不妨设为Φ0，即有Φ0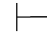0α.

如果有Φ的一个有穷子集Φ0，使得Φ0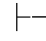0α，那么因为Φ0⊆Φ，由性质1可得：Φ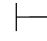0α.

性质4 如果Φ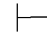0α，并且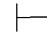0α→β，那么Φ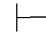0β.

证明 如果Φ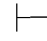0α，那么存在一个假设性证明，不妨设为π1，而α是π1的最后一步得出的公式，并且所有未被消除的假设都属于Φ，即

又因为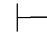0α→β，所以存在一个证明，不妨设为π2，并且α→β是π2的最后一步得出的公式，且没有未被消除的假设，即

如果把π2写在π1的最后一个公式α的下面，在π2的最后一个公式α→β下面写下β，就得到一个假设性证明π，公式β为π的最后一步得出的公式，且所有未被消除的假设都属于Φ，即

根据可演绎的定义得：Φ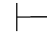0β.

性质5 Φ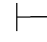0α，当且仅当Φ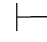0⇁⇁α.

证明 如果Φ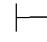0α，并由第三章第五节的定理5.6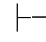：0α→⇁⇁α，由性质4可得：Φ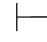0⇁⇁α.反之，如果Φ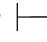0⇁⇁α，又由第三章第五节定理5.7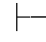：0⇁⇁α→α，由性质4可得：Φ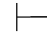0α.

性质6 如果Φ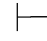0β并且Φ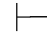0⇁β，那么对任意的公式α，都有Φ0α.

证明 因为Φ0β，所以存在一个假设性证明，不妨设为π1，并且π1的最后一步是β；又因为Φ0⇁β，所以也存在一个假设性证明，不妨设为π2，并且π2的最后一步是⇁β.π1和π2中所有未被消除的假设都属于Φ.构造证明π如下：在β之下写π2，在⇁β之下接如下的一个证明，作为π的一个子证明：

这样就得到了一个证明π，如下图所示：π的最后一步得到α，并且所有未被消除的假设都属于Φ.根据可演绎的定义得：Φ0α.

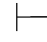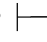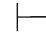性质7 Φ0α∧β，当且仅当Φ0α并且Φ0β.

证明 （1）如果Φ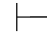0α∧β，由第三章第五节5.24和定理5.25，即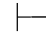：0α∧β→α和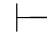0（α∧β）→β，再由性质4可得Φ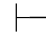0α并且Φ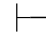0β.（2）如果Φ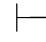0α并且Φ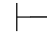0β，那么分别存在假设性证明π1和π2，使得在π1的最后一步得出α，在π2的最后一步得到β，而且所有未被消除的假设都属于Φ.即：

然后，把π2写在α之下，再在β之下写

这样就得到了一个证明π，它的最后一步是α∧β，并且所有未被消除的假设都属于Φ（如下图所示）.根据可演绎的定义可得：Φ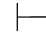0α∧β.

性质8 （1）如果Φ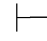0α，那么Φ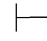0α∨β.

（2）如果Φ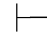0β，那么Φ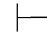0α∨β.

证明 因为Φ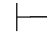0α，根据可演绎的定义得，存在一个假设性证明π，π的最后一步得出的公式是α或β，并且所有未被消除的假设都在Φ中.因此，只要在π之下，按照∨+规则接着写一个公式α∨β，该证明π′就是由Φ得到α∨β的一个证明.如下图所示.

性质9 如果Φ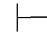0α→β且Φ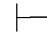0α，那么Φ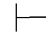0β.

证明 因为Φ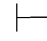0α→β并且Φ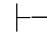0α，根据可演绎的定义可得：存在假设性证明π1和π2，并且在证明的最后一步分别是公式α→β和α，而所有未被消除的假设都属于Φ.即

构造非假设性证明π如下：

在证明π1的最后一个公式α→β之下，紧接着写下π2，再接着π2的最后一个公式α之下，写如下两个公式：

因为π的最后一步得出公式β，而且π中所有未被消除的假设都属于Φ.根据可演绎的定义，有Φ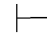0β.

性质10 如果Φ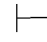0α→β，那么Φ，α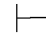0β.(www.daowen.com)

证明 因为Φ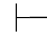0α→β并且Φ⊆Φ∪{α}（即：Φ⊆Φ，α）.由性质1得：Φ∪{α}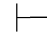0α→β，即：Φ，α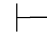0α→β.又α∈Φ∪{α}，所以，由性质2得：Φ∪{α}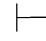0α，即：Φ，α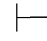0α.用性质9可得Φ，α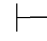0β.

性质11 如果Φ，α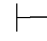0β，那么Φ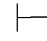0α→β.

证明 因为Φ，α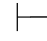0β，根据可演绎的定义得：存在一个假设性证明π1，π1的最后一个公式是β，并且所有未被消除的假设都属于Φ，α.

在π1中，把形如

而α未被消去的子证明都换成如下的子证明：

在π1的最后一个子证明中，用Hyp规则引入的假设或是α或不是α.如果是α，那么按上面的规定，π1的最后一个子证明被换为

这样就得到一个证明π2，而π2的最后一个公式就是（α→β），并且所有未被消除的假设都属于Φ，根据可演绎的定义，有Φ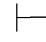0α→β.

如果在π1的最后一个子证明中，用Hyp规则引入的假设不是α，不妨设为

根据第三章第五节定理5.79，即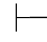0β→α→β，因此就存在一个证明π3，它的最后一个公式就是β→α→β.把π3接在π1的公式β之下，再在β→α→β之下写α→β，即

于是就得到一个证明π，即

它的最后一个子证明（γ之前）的部分是将π1中把形如

而α未被消除的子证明换为子证明

而得.

π的最后一个公式是（α→β），并且所有未被消除的假设都属于Φ，根据可演绎的定义，有Φ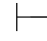0α→β.

性质11也称为命题逻辑的演绎定理.即：给定β的一个从Φ，α而来的演绎，我们就能构造α→β的一个从Φ而来的演绎.换句话说，如果我们想要构造α→β的一个从Φ而来的演绎，那么只要构造β的一个从Φ，α而来的演绎即可.

性质12 Φ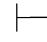0α，当且仅当有Φ的有限多个公式φ0，φ1，…，φn 满足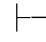0（φ 0→（φ1→…→（φn→α））…）.

证明 由性质3知：Φ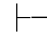0α，当且仅当Φ有一个有限子集Φ0，使得Φ0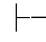0α.令Φ0={φ0，φ1，…，φn }，由性质10和性质11，得

性质13 如果Φ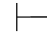0α并 且Φ，α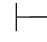0β，那么Φ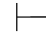0β.

证明 因为Φ，α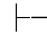0β.由性质11可得：Φ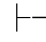0α→β.又因为Φ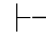0α，由性质9得：Φ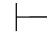0β.

性质14 如果Φ，α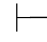0β，并且Φ，⇁α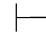0β，那么Φ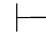0β.

证明 因为Φ，α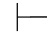0β，并且Φ，⇁α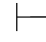0β，由性质11得：Φ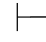0α→β和Φ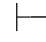0⇁α→β.利用第三章第五节定理5.86，即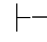0（α→β）→（⇁α→β）→β.于是，由性质4得：Φ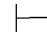0（⇁α→β）→β.再由性质9得：Φ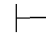0β.

性质15 如果Φ，⇁α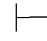0β并且Φ，⇁α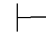0⇁β，那么Φ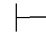0α.

证明 因为Φ，⇁α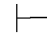0β并且Φ，⇁α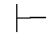0⇁β，由性质11可得：Φ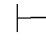0⇁α→β，并且 Φ 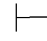0⇁α→⇁β.利用第三章第五节定理5.81，即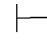：0（⇁α→β）→（⇁α→⇁β）→α.再由性质4和性质9可得：Φ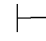0α.

性质16 如果Φ，α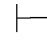0γ并 且Φ，β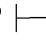0γ，那么Φ，α∨β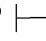0γ.

证明 因为Φ，α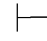0γ并 且Φ，β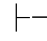0γ，那么由性质11可得：Φ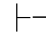0α→γ并且Φ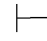0β→γ.利用第三章第五节定理5.83，即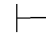0（α→γ）→（（β→γ）→（α∨β→γ））.再由性质4和性质9可得：Φ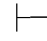0α∨β→γ，再由性质10得：Φ，α∨β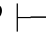0γ.

性质17 Φ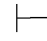0α↔β，当且仅当Φ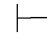0α→β并且Φ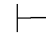0β→α.

证明 如果Φ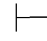0α↔β，用第三章第五节定理5.12和定理5.13，即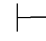0（α↔β）→α→β及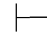0（α↔β）→β→α，由性质4得：Φ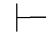0α→β及Φ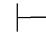0β→α.

如果Φ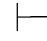0α→β及Φ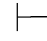0β→α，由第三章第五节定理5.72，即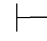0（α→β）→（β→α）→（α↔β）.由性质4和性质9得：Φ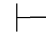0α↔β.

性质18 （1）如果Φ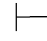0α↔β并且Φ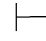0α，那么Φ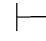0β.

（2）如果Φ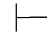0α↔β并且Φ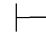0β，那么Φ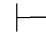0α.

证明 （1）因为Φ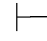0α↔β，利用第三章第五节定理5.12，即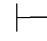0（α↔β）→α→β，由性质4得：Φ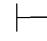0α→β，又因为Φ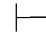0α，由性质9得：Φ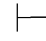0β.

（2）因为Φ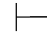0α↔β，利用第三章第五节定理5.13，即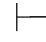0（α↔β）→β→α，由性质4得：Φ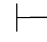0β→α，又因为Φ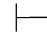0β，由性质9得：Φ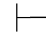0α.