在本章中，我们将讨论系统本身的一些性质.这些性质包括：可演绎性、相容性、可靠性、完全性和独立性.特别要证明公理系统PC和自然推理系统FPC的等价性.最后，还将给出公理系统PC的独立性证明.

相容性或协调性要求：在一个形式系统中不能既推出命题α，同时又推出它的否定⇁α.也就是说，在一个形式系统中绝不允许命题α与⇁α同真.因此，相容性的要求是对形式系统的一个基本要求.

可靠性要求：在一个形式系统中，所有可证的公式都是重言式.即：如果，那么0α.

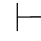完全性要求：在一个形式系统中，所有重言式都是该系统中的可证公式.即：如果0α，那么0α.

重言式是一个语义的概念，可证公式是一个语法的概念.可靠性和完全性从不同的角度刻画了这二者之间的关系.因此，我们有

定理1 在PC（或FPC）系统中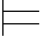，0α当且仅当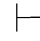0α.

这一结论还可以推广为：(www.daowen.com)

定理2 对任意的公式集Φ，和任意的公式α：Φ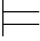0α当且仅当Φ0α.

独立性是指：在一个公理系统中，如果叫做公理的公式α不能根据给定的推演规则从其他的公理推演出来，称α是独立于其他公理或α是独立的.一个公理系统具有独立性是指：系统的每一公理都是独立的.因此，一个具有独立性的公理系统，其中每一条公理都是不可缺少的.

关系自然推理系统FPC和公理系统PC之间的关系，我们有下面的结论：

定理3 对任一公式α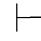，FPCα当且仅当PCα.即：自然推理系统FPC和公理系统PC是等价的.亦即：它们具有相同的定理.

我们将在第六章第五节中，详细证明自然推理系统FQC和公理系统QC的等价性.而FQC和QC是由FPC与PC分别加进关于量词的规则和公理而得到的一阶逻辑的自然推理系统和公理系统.因此，我们只要去掉证明中关于量词规则的部分，就可以得到FPC和PC等价性的证明.故此章略去该定理的证明.