现在,我们从语义的角度给出重言式和重言后承两个概念.这是两个非常重要的概念.
定义6.2 令Φ是一个公式集.如果对每个φ∈Φ,都有σ(φ)=1,那么称真值赋值σ满足Φ,记作σ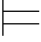 0Φ.特别地,当Φ={φ}时,记作σ
0Φ.特别地,当Φ={φ}时,记作σ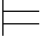 0φ,称真值赋值σ满足φ.
0φ,称真值赋值σ满足φ.
定义6.3 如果对任一公式α,并且对任意的真值赋值σ,都有σ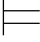 0α,那么称α为重言式.
0α,那么称α为重言式.
定义6.4 如果对于使σ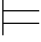 0Φ的每一真值赋值σ,都有σ
0Φ的每一真值赋值σ,都有σ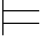 0α,那么称α是公式集Φ的重言后承,记作Φ
0α,那么称α是公式集Φ的重言后承,记作Φ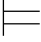 0α.特别地,当Φ为一空集时,记作
0α.特别地,当Φ为一空集时,记作 0α.当Φ={φ}时,记作φ
0α.当Φ={φ}时,记作φ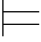 0α.
0α.
由以上定义立即可得出以下结论:
1.α是一个重言式,当且仅当∅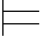 0α(α是空集的重言后承),当且仅当
0α(α是空集的重言后承),当且仅当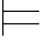 0α.
0α.
2.若α∈Φ,则Φ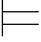 0α.
0α.
3.若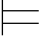 0α,则Φ
0α,则Φ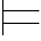 0α,即:重言式是任何公式集Φ的重言后承.
0α,即:重言式是任何公式集Φ的重言后承.
例6.2 证明:α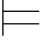 0α∨β,⇁α
0α∨β,⇁α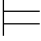 0α→β.
0α→β.
证明 对于任一真值赋值σ,如果σ(α)=1,则σ(α∨β)=max(σ(α),σ(β))=1;如果σ(⇁α)=1,则σ(α)=1-σ(⇁α)=0,由此得σ(α→β)=1.
例6.3 证明:如果Φ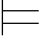 0α并且Φ
0α并且Φ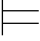 0α→β,则Φ
0α→β,则Φ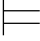 0β.
0β.
证明 对任意的真值赋值σ,如果σ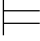 Φ,并且当σ(α)=σ(α→β)=1时,由真值赋值的定义,可得σ(β)=1.故:Φ
Φ,并且当σ(α)=σ(α→β)=1时,由真值赋值的定义,可得σ(β)=1.故:Φ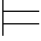 0β.
0β.
定义6.5 如果公式α和β互为重言后承,即对每个真值赋值σ,都有σ(α)=σ(β),那么称α和β是重言等值的.
定理6.1 {α1,α2,…,αn}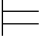 0α当且仅当
0α当且仅当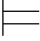 0α1→α2→…→αn→α.
0α1→α2→…→αn→α.
证明 只需证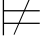 0α1→α2→…→αn→α当且仅当{α1,α2,…,αn}
0α1→α2→…→αn→α当且仅当{α1,α2,…,αn}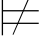 0α即可.事实上,
0α即可.事实上,
当且仅当 σ(α1→α2→…→αn→α)=0,
当且仅当 σ(α1)=1,σ(α2→α3→…→αn→α)=0,(https://www.daowen.com)
当且仅当 σ(α1)=σ(α2)=1,σ(α3→α4→…→αn→α)=0,
⋮
当且仅当 σ(α1)=σ(α2)=…=σ(αn)=1,σ(α)=0,
当且仅当 {α1,α2,…,αn}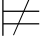 0α.
0α.
定理6.2 Φ,α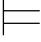 0β当且仅当Φ
0β当且仅当Φ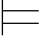 0α→β.
0α→β.
证明 设Φ,α 0β并且设σ是任意的使Φ中每个公式都为1的真值赋值.
0β并且设σ是任意的使Φ中每个公式都为1的真值赋值.
如果σ(α)=1,则由Φ,α 0β可得σ(β)=1.于是,σ(α→β)=1;如果σ(α)=0,则σ(α→β)=1.由此证得Φ
0β可得σ(β)=1.于是,σ(α→β)=1;如果σ(α)=0,则σ(α→β)=1.由此证得Φ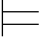 0α→β.
0α→β.
反之,设任意的真值赋值σ,σ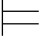 0Φ且σ
0Φ且σ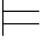 0α,又Φ
0α,又Φ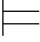 0α→β.所以对所有满足Φ和α的真值赋值σ,都有σ
0α→β.所以对所有满足Φ和α的真值赋值σ,都有σ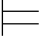 0α→β.再由真值赋值的定义可得:σ
0α→β.再由真值赋值的定义可得:σ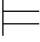 0β.即:Φ,α
0β.即:Φ,α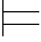 0β.
0β.
定理6.3 对任意的公式α和β,有{α,α→β}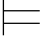 0β.
0β.
证明 利用定义6.1,可立刻得此结论.
定理6.4 α与β重言等值当且仅当(α↔β)是重言式.
证明 α与β重言等值,当且仅当对任意的真值赋值σ,都有σ(α)=σ(β),当且仅当对任意的真值赋值σ,有σ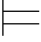 0α↔β,当且仅当α↔β为重言式.
0α↔β,当且仅当α↔β为重言式.
这一节,我们又从语义学的角度刻画了重言式和重言后承的概念.重言后承是命题逻辑中前提和结论之间关系的语义刻画.它说明在前提为真的条件下可以得出什么样的结论,即刻画了前提与结论之间的真假关系.这两个概念都是从可真性引出的.在本章第二、三、四节中,我们已从语法的角度描述了这两个概念,即从可证性描述了它们.
如果在一个系统里可证的公式都是重言式,即若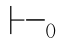 α,那么
α,那么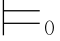 α,则称该系统是可靠的.反之,如果一个公式是重言的,那么它也是可证的,即若
α,则称该系统是可靠的.反之,如果一个公式是重言的,那么它也是可证的,即若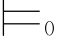 α,那么
α,那么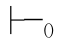 α,则称该系统是完全的.如果一个系统同时具有这两个特性,那么它恰好包罗了全体重言式.这样的系统从逻辑的角度说是一个好系统,因为在这样的系统里,一个推理是否正确在系统中完全能判明.正确的推理所相应的蕴涵式在这个系统中都是可证公式;如果推理的蕴涵式在系统中不可证,那么推理就是不正确的.PC系统和FPC系统都是这样的系统,它们既具有可靠性又具有完全性.另外,PC系统和FPC系统也是协调的,即不存在一个公式α,使得
α,则称该系统是完全的.如果一个系统同时具有这两个特性,那么它恰好包罗了全体重言式.这样的系统从逻辑的角度说是一个好系统,因为在这样的系统里,一个推理是否正确在系统中完全能判明.正确的推理所相应的蕴涵式在这个系统中都是可证公式;如果推理的蕴涵式在系统中不可证,那么推理就是不正确的.PC系统和FPC系统都是这样的系统,它们既具有可靠性又具有完全性.另外,PC系统和FPC系统也是协调的,即不存在一个公式α,使得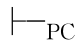 α,⇁α,或者
α,⇁α,或者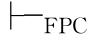 α,⇁α.(这些结论,将在第四章讨论)
α,⇁α.(这些结论,将在第四章讨论)
值得注意的是:α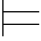 0β和α
0β和α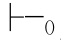 β中的关系
β中的关系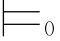 和
和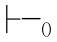 不同.前者是语义的,表明公式α和β之间的真假关系,而同演绎系统中的公理和推理规则无关;后者是语法的,表示根据演绎系统中的公理和推理规则,从α能推导出β,而与对公式的赋值以及真假无关.但是,根据命题演算的完全性和可靠性,有α
不同.前者是语义的,表明公式α和β之间的真假关系,而同演绎系统中的公理和推理规则无关;后者是语法的,表示根据演绎系统中的公理和推理规则,从α能推导出β,而与对公式的赋值以及真假无关.但是,根据命题演算的完全性和可靠性,有α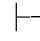 0β当且仅当α
0β当且仅当α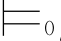 β,从而表明:在命题逻辑中,
β,从而表明:在命题逻辑中,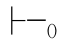 精确严格地表达了
精确严格地表达了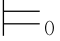 ;反之亦然.换句话说,命题语义学的目的就是给命题演算关系
;反之亦然.换句话说,命题语义学的目的就是给命题演算关系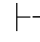 0做出一种有意义的描述;反之,命题演算的目的就是要通过建立适合的形式系统,对语义后承关系
0做出一种有意义的描述;反之,命题演算的目的就是要通过建立适合的形式系统,对语义后承关系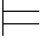 0做出一种语法描述.
0做出一种语法描述.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






