自然推理系统的出发点除了语言部分与公理系统相同外，只是一些用模式给出的推理规则.FPC系统的推理规则分两类，它们是：结构规则和逻辑联结词规则.
1.结构规则
（1）Hyp（假设引入规则）
这条规则允许：按需要随时可引入一个假设.
（2）Rep（重复规则）
这条规则允许：在一个假设下出现的公式（包括假设）可重复出现.
（3）Reit（重述规则）
这条规则允许：在一个假设下出现的公式（包括假设）可在随后的假设下重复出现.
这些规则可图示如图3-1。
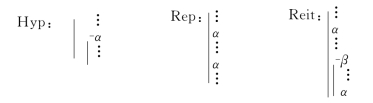
图3-1
2.逻辑联结词规则
（1）→+（→引入） 如果在α的假设下，可得到β，则可推出α→β.
（2）→-（→消去） 从α和α→β可推出β.
（3）∨+（∨引入） 从α可推出α∨β；从α可推出β∨α.
（4）∨-（∨消去） 从α∨β，α→γ和β→γ可推出γ.
（5）∧+（∧引入） 从α和β可推出α∧β.
（6）∧-（∧消去） 从α∧β可推出α；从α∧β可推出β.
（7）↔+（↔引入） 从α→β和β→α可推出α↔β.
（8）↔-（↔消去） 从α↔β和α可推出β；从α↔β和β可推出α.或者从α↔β可推出α→β；从α↔β可推出β→α.
（9）⇁（⇁规则） 如果在⇁α的假设下，可得到β和⇁β，则可推出α.
这些规则的图示如图3-2.
图3-2
→+规则可记作：若α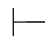
β，则
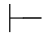α→β.实际上，应该记作若α
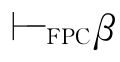，则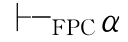
→β.在不引起混淆的情况下，我们略去下标FPC，以下均同.这条规则表示：如果要证明形状为α→β的公式，则可先假设α，再证由α可推出β.如果实现了这一步，则可说α→β得证.这是演绎推理中的演绎定理.
→-规则可记作：α→β，α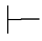
β.它表示：由α→β和α，可得β.这反映了演绎推理中的假言推理原则.(www.daowen.com)
∨+规则可记作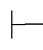：α
α∨β，α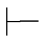
β∨α.它表示：由α可得α∨β；由α可得β∨α.这是演绎推理中选言推理的反映.
∨-规则可记作：α→γ，β→γ，α∨β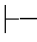
γ.它表示：如果要证明α∨β可推出γ，还要证α和β分别可推出γ.实现了这一步，才可以说α∨β推出γ.这是演绎推理中二难推理的反映.
∧+规则可记作：α，β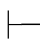
α∧β.即从α和β能得出α∧β.这是演绎推理中联言推理的反映.它表示：从α和β真可得α∧β真.
∧-规则可记作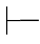：α∧β
α，α∧β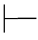
β.它也叫联言分解式，表示由α∧β可得α，也可得β.这也是演绎推理中联言推理的反映.
↔+规则可记作：α→β，β→α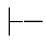
α↔β.它表示由α→β和β→α可得α↔β.这是演绎推理中既充分又必要的条件，是充分必要条件.
↔-规则可记作：α↔β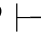
α→β，α↔β
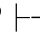β→α.它表示由α↔β可得α→β和β→α.这反映了演绎推理中的充分必要条件既是充分条件又是必要条件.
⇁规则可记作：若⇁α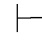
β，⇁β，则
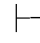α.它表示在⇁α的假设下，如果得出一对矛盾的公式，则可消去⇁α得到α.这一规则也就是反消规则.它反映了演绎推理中的反证法.
上述九条规则又可以分为两类：一类直接表示前提和结论之间的推理关系，如→-规则表示：从前提α→β和α可推出结论β.这一类规则称为第一类规则.另一类规则不是直接表示前提和结论之间的推理关系，而是说如果某个推理关系成立，则另一个推理关系也成立，如→+规则表示：如果推理关系α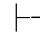
β成立，则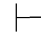
α→β也成立.这一类规则称为第二类规则.
FPC系统的一个证明就是依上述两类规则构造出来的一系列公式.如果一个证明结束于某个假设下，则称该证明为假设性证明（即在每个假设下，并未都用了⇁规则或→+规则）.否则，称该证明为非假设性证明.当公式α是某个非假设性证明的最后一步时，称α是（形式）可证的公式，或称α是FPC的定理，记作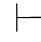
α，并称该证明为α的一个（形式）证明.
下面我们将以PC系统的四条公理为例，说明FPC系统中可证公式的证明方法.
例4.1 在FPC中，证明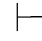
α∨α→α.
证明
例4.2 在FPC中，证明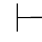
α→α∨β.
证明
例4.3 在FPC中，证明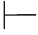
α∨β→β∨α.
证明
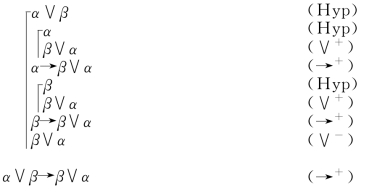
例4.4 在FPC中，证明
（β→γ）→（α∨β→α∨γ）.
证明
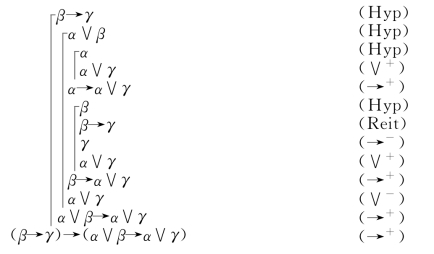
从上面的4个例子可以看出，FPC的一个证明是利用上述规则构造出来的一个有穷公式序列.一个证明中每个假设下的一系列公式（包括假设）称为该证明的一个子证明.每个子证明的开始用一横一竖标出（即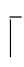
，它起括号的作用）.横线的右边是该子证明的假设，竖线画到该子证明的最后一个公式的上端，表示整个非假设性证明（即不是终止于某个假设下的证明）的那个横上为空（没有公式），标志无假设.在例④中，从α∨β到α∨γ的一列公式是在假设β→γ下的一个子证明，从α到α∨γ和从β到α∨γ是在假设α∨β下的两个子证明。但是，从α到α→α∨β的一列公式和从β和β→α∨γ的一列公式构成两个非假设性证明。同样，从α∨β到α∨β→α∨γ和从β→γ到（β→γ）→（α∨β→α∨γ）也都是非假设性证明.每个子证明的标志
分别依次右移.作出几个可能的假设时，这些假设下的子证明排在一列.
从本章第三节和第四节看出，PC系统和FPC系统形式各异，两个系统中的“可证公式”的意义也不相同.但我们能够证明：FPC系统中的可证公式也是PC系统中的可证公式；反之，PC系统中的可证公式也是FPC系统中的可证公式.在这个意义上，命题演算的自然推理系统FPC和公理系统PC是等价的.等价性证明留在下一章完成.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
