在对一个公理系统的研究过程中，人们所关心的主要问题是：在系统的公理和推理规则给定之后，根据这些公理和规则能够推演出哪些定理，能够推出多少定理以及如何推演定理.现在，我们的任务就是要利用PC的公理和推理规则，将其余的“重言式”找出来.这个推演的过程叫证明，其定义如下：

定义3.1 满足下面两个条件之一的公式所组成的有穷公式序列φ1，φ2，…，φn称为本系统的一个证明.

（1）φi（i=1，2，…，n）是公理之一；

（2）φi是由序列中排在前面的两个公式运用MP规则得到的，或者由序列中排在前面的一个公式运用定义得到的.证明的有穷公式序列的最后一个公式φn如果是α，那么称该证明是公式α的一个证明，或说α是可证的，记作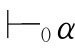，并称α是本系统的一个定理.在不引起混淆时，也记作α.

一般情况下，我们有如下的定义：

定义3.2 设α是任一公式，Φ是任一公式集.如果存在一个有穷的公式序列，其末项是公式α，而且该序列中的每个公式或是一个公理，或是属于Φ，或是由排在前面的两个公式应用MP规则得到的，或者由序列中排在前面的一个公式运用定义得到的.那么称公式α是从公式集Φ可演绎的，记作Φ.当Φ=∅时，即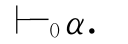

PC系统有下面的定理：

定理1和定理2分别被称为命题演算PC中的三段论原则和同一原则.定理3和定理4均被称为命题演算PC中的排中律.定理5是命题演算的双重否定原则，定理6是它的逆.定理7是命题演算的假言易位原则.定理8和定理9统称为命题演算PC的合取否定的德·摩根律.定理10被称为析取的左附加原则.

下面证明定理1.

现在我们能用的工具只有公理和推理规则.为了证明定理1，我们首先观察它的形状与哪条公理相似，然后确定使用的工具.通过观察发现，只要在公理A4中将α换成⇁α即可.于是，关于定理1，我们有如下的证明.

在以后的证明中，除公理和MP规则以外，定理1也可作为证明的工具使用.这一点与数学中的定理一样.(www.daowen.com)

下面证明定理2.

为了证明它，我们不妨取定理1中的γ为α.这样一来，定理1就变形为（（β→α）→（α→β）→（α→α））.可以看出，我们只要适当选取β，使得前件β→α和α→β恰好是公理.于是，使用两次MP规则，就可以得到定理2.现在的问题是：β取什么，才能将前件β→α和α→β分离掉.通过把它们与公理A1和公理A2比较发现，取β为α∨α即可.于是关于定理2我们有如下证明：

下面证明定理3.

下面证明定理4.

下面证明定理5.

下面证明定理6.

定理7的证明：

定理8的证明：

定理9的证明：

定理10的证明：