定义甲：（α∧β）被定义为⇁（⇁α∨⇁β）.

定义乙：（α→β）被定义为（⇁α∨β）.

定义丙：（α↔β）被定义为（（α→β）∧（β→α））.

有了定义甲、乙、丙，我们就可以将（α∧β）作为符号序列⇁（⇁α∨⇁β）的缩写，将（α→β）作为符号序列（⇁α∨β）的缩写，将（α↔β）作为符号序列（（α→β）∧（β→α））的缩写.

定义 公式α中T和F的每次出现加0，⇁的每次出现加1，∨、∧、→和↔的每次出现加2所得的和数称为公式α的复杂度，记作deg（α）.

如果在公式α中出现∧，→和↔，规定：它们的每次出现加2.

为了阅读和书写的方便，我们有时可能省略各种括号.括号的省略规则，仍与第二章规定的一致.从严格意义上讲，这些省略了括号的符号或符号序列本身并不是公式.

如果令L0的全体公式组成的集合为W0，则有以下引理.

引理 一个公式集S是W0的充要条件是：

（1）如果α是原子公式，则α∈S；

（2）如果α∈S，则⇁α∈S；

（3）如果α，β∈S，则（α∨β）∈S.

证明 由L0的形成规则，必然性显然成立.下面证明定理的充分性.如果S满足条件（1）～（3），而S≠W0，则必有一公式αS.由（1），α必是复合公式.令

S′={n|n∈Z+并且n=deg（α）并且αS}.(www.daowen.com)

设m是S′的最小元.因此凡复杂度小于m的公式均属于S，且至少有一个复杂度为m的公式不属于S.不妨设为α.α只可能是下面的两种情况之一：

①α形如⇁β

因为deg（β）=m-1，所以β∈S.由（2）可得⇁β∈S，即α∈S，这与αS矛盾.

②α形如（β∨γ）

因为deg（β）＜m并且deg（γ）＜m，所以β∈S并且γ∈S.由（3）可得（β∨γ）∈S，即α∈S，这与α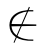S矛盾.

由以上的证明可知，S满足（1）～（3），而S≠W0是不可能的.故如果满足（1）～（3）条，则S=W0，证毕.

一切合式公式，不论其构成多么复杂，都是根据形成规则构成的.由前面的引理，如果我们要证明每个合式公式α具有某性质φ，只需证明下面的定理.

定理 一切合式公式α均有性质φ，如果满足：

（1）原子公式都具有性质φ；

（2）如果α具有性质φ，则⇁α具有性质φ；

（3）如果α和β都具有性质φ，则（α∨β）也具有性质φ.

证明 利用前面的引理，详细证明留给读者.