一个真值形式不论多么复杂，我们都可以用真值表方法，判断它是否一个重言式.但是，当真值形式的构造比较复杂，或者所含命题变项的个数比较多时，构造它的真值表就是一件比较麻烦的事情.为此，这里给出两种比较简便的判定方法.一种是简化真值表方法，也叫赋值归谬法；另一种是真值树方法.它们都是以真值表方法为基础的.

（1）简化真值表方法

简化真值表方法特别适合于主联结词是“→”的蕴涵式.因为在p→q的真值表中，只有当p真q假时，p→q为假.如果一个蕴涵式是重言式，那么，在该蕴涵式中不能出现前件真而后件假的情况.换句话说，不论该蕴涵式中的命题变项各取什么值，都不能使它的前件为真、后件为假.这种方法就是归谬法.具体作法是：假定所给蕴涵式的值为假.于是可得所给蕴涵式前件的值为真，后件的值为假.在这种赋值下，如果能导致矛盾的结果，就证明了该蕴涵式不能取假值，因此要判定的蕴涵式就是一个重言的蕴涵式.如果不能导致矛盾的结果，那么所要判定的蕴涵式就不是一个重言式.所以，把这种方法叫赋值归谬法.下面将结合具体例子说明简化真值表方法的使用.

例2.19 用简化真值表方法判定：p→p∨p是否重言式.

解

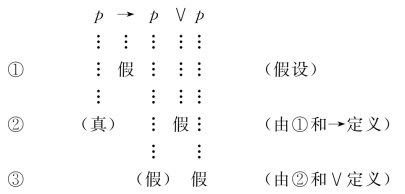
由②得p真，由③得p假，矛盾！所以，假设p→p∨p为假不成立.故：p→p∨p是一个重言式.

例2.20 用简化真值表方法判定：p∨q→q∨p是重言式.

解

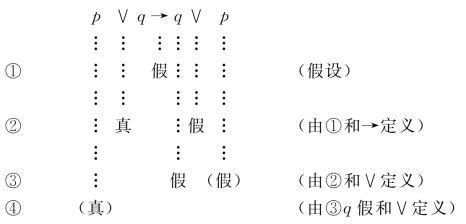
由③p假且q假，将q假代入前件得p真，矛盾！故：p∨q→q∨p为一重言式.

例2.21 用简化真值表方法判断：（p→q）∧⇁p→⇁q是否重言式.

当p假q真时，（p→q）∧⇁p→⇁q为假，故：该蕴涵式不是重言式.我们不妨用它的真值表进行检验.

由此看出，当p假q真时，该公式的值为假.因此，它不是重言式.

在使用简化真值表方法时，如果遇到⇁为真或假，∨和→为假，∧为真时，计算就能一直进行下去.否则，需要分情况进行讨论.如：

例2.22 用简化真值表方法判定：p→p∧p是否重言式.

显然，不论（i）～（iii）哪一种情况发生，p的值都既真又假，矛盾！所以，p→p∧p是一个重言式.

例2.23 同例2.20.

如果（i）成立，即

由此可得：p既真又假，矛盾！

如果（ii）成立，即

由此可得：p既真又假，矛盾！

如果（iii）成立，即

由此可得：p既真又假，矛盾！

因此，不论（i）～（iii）哪一种情况出现，都将得到矛盾的结果.故：p∨q→q∨p是一个重言式.

用简化真值表方法判断一个真值形式是否重言式的方法在记法上还可以再简单一些.用下面的（1）和（2）来说明.

以上两例中最下面一行的数字1，2，…表示判定步骤的第一步，第二步，……通常可以省略.带有圈的真或假表示它们是矛盾的赋值.其中（1）的赋值出现了矛盾，说明（1）不能为假，因此它是一个重言式.（2）的赋值没有出现矛盾，说明我们找到了一种赋值（p假，q真），使该公式为假.由于（2）式可以为假，所以（2）不是重言式.

总之，简化真值表的基本作法大致可以归结为以下四步：

第一步：假设要判定的公式为假，即在其主联结词（蕴涵词）下置假；

第二步：根据真值表对其子公式赋值，即在这些子公式的主联结词下置真或假.必要时可以对所有的子公式都给出赋值.

第三步：一旦出现相同的命题变项（或子公式）既需置真又需置假，则出现矛盾.因此，对这样的真或假画圈.

第四步：根据所赋的真值真或假是否出现圈，最后得到判定结果.

（2）真值树方法

真值树方法也是一种用来判定一个真值形式是否重言式的方法.在很多场合中，它比真值表方法和简化真值表方法更有效.

真值树的形状像一棵倒置的树.我们将它记作T.它的元素叫结点.每个结点上都放有一个有穷的公式集.如图2-1所示.每个结点属于唯一的一层，层可以用自然数标明.图2-1所示的真值树有三层，我们说这棵树的深度为3.这里Φij（i，j=0，1，2，3）是任意有穷的公式集.Φ00叫真值树T的始点，Φ21叫Φ11的后继，Φ31叫树T的一个终点.由Φ00，Φ11，Φ21，Φ31组成的这条通道叫树T的一个分枝.不同结点上的公式集既可以相同，也可以不同.一棵树有几个终点，就有几个分枝.单个的Φ00也叫一棵（退化的）真值树.它既是始点又是终点，它的结点只有一个.所以，这棵树只有一个分枝，就是它自身.

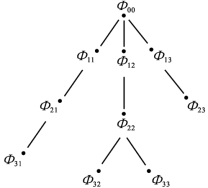
图2-1

下面，我们规定真值树T长出新枝的规则：

⇁⇁规则：如果在树T的一个终止于结点Φ的分枝的公式之中有一个公式⇁⇁α，则附加一个新的结点{α}作为Φ的后继，如图2-2所示.

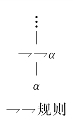
图2-2(www.daowen.com)

→规则：如果在树T的一个终止于结点Φ的分枝的公式之中有一个公式α→β，则附加两个新的结点{⇁α}和{β}作为Φ的后继，如图2-3所示.

图2-3

⇁→规则：如果在树T的一个终止于结点Φ的分枝的公式之中有一个公式⇁（α→β），则附加一个新的结点{α，⇁β}作为Φ的后继，如图2-4所示.

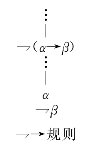
图2-4

注意：①不一定只在分枝的终点上才使用上述三条规则.②使用⇁⇁规则和⇁→规则时，真值树不分岔，使用→规则时，真值树分岔.③一般情况下，先使用不分岔的规则.

例2.24 作α→⇁（⇁⇁β→α）的真值树.

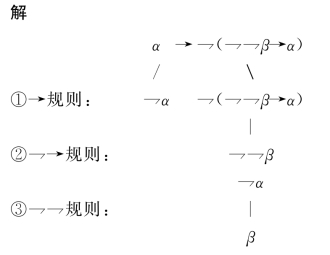
这棵树的深度是3，并且它有两个分枝.对公式α→⇁（⇁⇁β→α）或⇁（⇁⇁β→α）或⇁⇁β还可以再分别使用规则→，⇁→和⇁⇁.但继续使用这些规则，产生不出新的公式.因此，在这种情况下，我们就不再继续使用这些公式来扩充此真值树.但要求在该公式旁画钩，即√，以表示该公式已使用过了.于是，我们规定：

定义2.4 如果下列三个条件之一成立，那么称在某一分枝的某个公式φ在该分枝中用过了：

（1）如果φ是⇁⇁α，并且α是该分枝的公式；

（2）如果φ是α→β，并且⇁α或β是该分枝的公式；

（3）如果φ是⇁（α→β），并且α和⇁β二者同为该分枝的公式.

因此，构造真值树时，在一个分枝中，用过的公式就不必再用来扩张.当对一个公式使用某个规则扩张树时，最好的作法是立即用它扩张它所属的一切分枝.

定义2.5 在树T的一个分枝中，若有一个公式α，使得α和⇁α都是该分枝的公式，则称T的该分枝是封闭的.公式α和⇁α叫做用来封闭该分枝的公式.对封闭的分枝，在该分枝的下方打叉，即×.

定理 公式集Φ的一棵树T被称为Φ的一个反驳，如果它的所有分枝都是封闭的.反驳Φ就是构造Φ的一个反驳.特别地，如果⇁α能被反驳，则α是一个重言式.

这里略去该定理的证明.有兴趣的读者请参阅文献[8].

例2.25 用真值树方法证明：p→p是一个重言式.

证明 由上述定理，只需构造⇁（p→p）的一个反驳.

因为我们能构造⇁（p→p）的一个反驳，故p→p是一个重言式.

例2.26 用真值树方法证明α是一个重言式.

α：（q→r）→（（p→q）→（p→r））.

证明 现在构造⇁α的一个反驳：

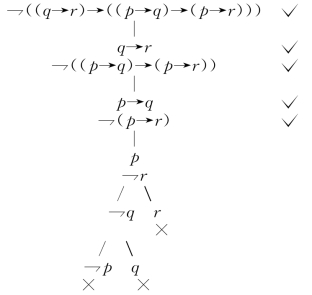
因为我们能构造⇁α的一个反驳，所以α是一个重言式.

我们在构造⇁α的一个反驳时，也可以先使用分岔的规则.不过这样做，通常情况下，树杈较多，树枝封闭得较晚.如：

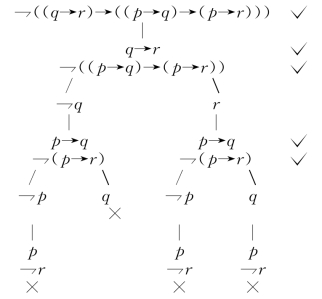
由此可知：一个公式α的真值树不是唯一的.

由联结词∨，∧和↔构成的公式，可根据以下的三个重言等值式：

（α∨β）↔（⇁α→β），

（α∧β）↔⇁（α→⇁β），

（α↔β）↔（α→β）∧（β→α），

将它们转换成只用联结词⇁和→表达的公式，然后再使用规则⇁⇁，⇁→和→来构造它们所对应的真值树.也可以从⇁⇁规则、⇁→规则和→规则中推导出它们的规则.图2-5是它们的导出规则.

图2-5

例2.27 用真值树方法证明α′是一个重言式.

α′：（α→β）∧（β→α）→（α↔β）.

证明 现在构造⇁α′的一个反驳：

因为我们能构造出⇁α′的一个反驳，所以α′是一个重言式.

例2.28 用真值树方法判断α是否重言式.

α： p→（p∧（p→q））.

证明 构造⇁α的一棵树：

因为在⇁α的真值树中，有一分枝不封闭，因此，我们不能反驳⇁α，故α不是重言式.