1.下列关系中哪些能构成函数？

（1）F1={〈x1，x2〉|x1，x2∈Z+并且x1+x2＜20}，其中Z+为正整数集合；

（2）F2={〈y1，y2〉|y1，y2∈R并且y2=|y1|}，其中R为实数集合；

（3）F3={〈z1，z2〉|z1，z2∈R并且

2.求下列各关系的定义域和值域，并指出它们中的哪些是函数.

（1）R1={〈1，〈2，3〉〉，〈2，〈3，4〉〉，〈3，〈1，4〉〉，〈4，〈1，4〉〉}；

（2）R2={〈1，〈2，3〉〉，〈2，〈3，4〉〉，〈3，〈3，2〉〉}；

（3）R3={〈1，〈2，3〉〉，〈2，〈3，4〉〉，〈1，〈2，4〉〉}；

（4）R4={〈1，〈2，3〉〉，〈2，〈2，3〉〉，〈3，〈2，3〉〉}.

3.设f：A→B，g：A→B，并且f∩g≠∅，问f∩g和f∪g一定是函数吗？证明你的结论.

4.构造一个函数：

（1）从1到1； （2）从0到1； （3）从2×3到6，从6到2×3两个双射.

5.令BA={f|f：A→B}，构造下面的集合：

（1）23； （2）32； （3）20； （4）02； （5）00；

（6）10； （7）11； （8）01； （9）21； （10）12.(www.daowen.com)

6.下列函数中哪些是单射？哪些是满射？哪些是双射？

（1）f：N→N，f（n）=n2+2；

（2）f：N→N，f（n）=n除以3的余数；

（3）f：N→N，f（n）=

（4）f：N→N，f（n）=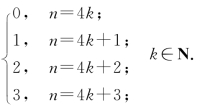

7.对于下面的每一对集合A和B，构造一个从A到B的双射.

（1）A={1，2，3}，B={a，b，c}；

（2）A=P（{a，b，c}），B={f|f：{a，b，c}→{0，1}的映射}.

8.设f：A→B是函数，R是A上的关系，并且满足：〈a，b〉∈R当且仅当f（a）=f（b）.证明R是A上的等价关系（我们称R是由函数f导出的等价关系）.

9.设f：R→R并且f（x）=x+3，g：R→R并且g（x）=2x+1，h：R→R并且h（x）=x/2.试求：g◦f，f◦g，f◦f，g◦g，f◦h，h◦g，h◦f，f◦h◦g的函数表达式.（这里R是实数集）

10.设f，g，h都是N到N的函数，并且f（n）=n+1，g（n）=2n，h（n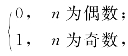）=试求：f◦f，f◦g，g◦f，h◦g，f◦g◦h的函数表达式.

11.证明：若A，B为有限集，则A×A，A B也是有限集.

12.用康托尔对角线方法证明：自然数的一切子集的个数比自然数集的元素的个数要多.

13.证明：如果，则