前面我们曾提到过元素的“个数”、“有限集”和“无限集”等概念.下面我们给出它们的严格定义.

定义4.7 对于任意的集合X，如果存在一个自然数n，使得X恰有n个元素，那么称X为有限集.如果集合X不是有限集，那么称X为无限集.

例4.5 ∅是有限集，它的元素个数是零.单元集{a}，{1}和{N}等都是有限集.{1，2，…，n}是有限集，它恰有n个元素.

有限集具有下面显然的性质：

（1）若X是有限集，则P（X）也是有限集；

（2）若X和Y都是有限集，则X∪Y，X∩Y，X-Y也都是有限集.

例4.6 自然数集合N是一个无限集.因为如果N是一个有限集，根据有限集的定义，存在一个自然数n，使得N恰有n个元素.由N的定义，0，1，2，…，（n-1）这n个元素都属于N，但n也是一个自然数，所以，n∈N.此与假设N有n个元素矛盾，这就证明了N是一个无限集.

例4.7 集合Z、Q、R都是无限集.

现在，我们来考察两个集合之间的关系.当两个集合X和Y都是有限集时，我们就可以分别去数它们的元素，从而知道它们的元素个数相等或是其中一个比另一个更多一些，甚至多出的数目也可以知道.当两个集合之一为无限集，另一个为有限集时，可以断定无限集比有限集的元素多.但是，当两个集合都是无限集时，怎样判断哪个集合的元素更多一些呢？例如，正整数集合X={1，2，…，n，…}与正整数平方的集合Y={1，4，9，…，n2，…}，这两个集合哪个集合的元素更多一些呢？这是1638年意大利天文学家伽利略遇到的一个问题.直到19世纪70年代，康托尔第一次系统地研究了无限集合的变量问题，并给出了变量集合的“一一对应”概念，才正确回答了伽利略的问题.

定义4.8 凡能与自然数集N一一对应的集合叫做可数无限集，简称可数集；把不能与自然数集N一一对应的无限集叫做不可数集.

由于N的元素可以排成如下的无穷序列的形式：

因此，我们可以将任意的一个可数集合A的元素排列成如下的形式：

反之，对于任意的集合A，如果它的元素可以排成上述式（2）的形式，则A一定是可数集.事实上，我们只要令它的第n个元素和自然数n对应即可.所以，一个无限集合是可数集当且仅当它可以排成式（2）的形式.

为了以后各章使用方便，下面证明可数集的一些重要性质.

定理4.1 任意的无限集合A，均包含一可数子集.

证明 因为A无限，所以，A≠∅.因此，我们可以从A中任取一个元素并记为a0，因为A是无限集，则A≠{a0}.于是便可在A中任取一元素a1≠a0.一般来说，设已挑出互不相同的元素：

a0，a1，…，an （ai∈A，i=0，1，2，…，n）.

又因A是无限的，所以A-{a0，a1，…，an}≠∅.因此，又可在A-{a0，a1，…，an}中任取一个元素an+1，它自然不同于a0，a1，…，an.由数学归纳法，我们得到一个由A中互异的元素作成的无限序列

a0，a1，…，an，….

显然A′={a0，a1，…，an，…}是可数的，并且A′⊆A.

定理4.2 可数集合的无限子集仍是可数集.

证明 设A可数，则A的元素可以排成如下的一个无限序列：

a0，a1，…，an，….

如果A′是A的一个无限子集，则所有属于A′的a其下标做成全体自然数集N的一个无限子集N′.由于N的任何无限子集都可按其元素的大小排成一个无限序列，因此N′是可数的，而N′和A′一一对应，所以A′也是可数的.

推论4.1 从可数集A中去掉一个有限集，所得的集合仍为可数集.

定理4.3 若A可数并且B有限，A∩B=∅，则A∪B可数.

证明 因为A可数，则A与N之间存在一一对应，不妨设A为：

a0，a1，a2，…，an，….

设B中有（m+1）个元素，即：B={b0，b1，…，bm}，由于A∩B=∅，则

A∪B={b0，b1，…，bm，a0，a1，…，an，…}，

因为A∪B可以排成无限序列的形式，因而可数.

定理4.4 若A，B都可数并且A∩B=∅，则A∪B亦可数.

证明 设A={a0，a1，a2，…，an，…}，B={b0，b1，…，bn，…}，因为A∩B=∅，所以

A∪B={a0，b0，a1，b1，…，an，bn，…}.

可见A∪B也是可数的.

推论4.2 设A可数，B有限或可数，则A∪B仍是可数的.证明 令B*=B-A∩B，则A∩B*=∅，而此时

A∪B=A∪B*.

因为B*或有限或可数，故由定理4.3或定理4.4知，A∪B可数.

推论4.2表明：定理4.3和4.4中条件A∩B=∅是可以取消的.

定理4.5 设有一列可数集A0，A1，…，Ai，…，且Ai∩Aj=∅（i≠j），则Ai也可数.

证明 因为Ai（i=0，1，2，…）可数，所以，设

用对角线方法，将的元素进行编号（记i+j=h为元素aij（i，j=0，1，2，…）的高度.于是，

故可数.

注：（1）如果把每个Ai改为有限集，其他条件不变，那么定理4.5仍成立.也就是说，两两不相交的可数个有限集的并集仍是一个可数集.

（2）如果在定理4.5中去掉两两不相交这一限制.Ai为可数集或有限集，则为可数集或有限集，特别地，我们有：(www.daowen.com)

推论4.3 若Ai（i=0，1，2，…）可数，则可数.

证明 令A*0=A0，

A*i=Ai-Ai∩（A0∪A1∪…∪Ai-1） （i≥1），

则A*i有限或可数，并且A*i∩A*j=∅（i≠j），则

故可数.

推论4.3表明：可数个可数集的并集还是可数集.

定理4.6 有理数集Q是可数的.

证明 设，则Ai是可数集，由推论4.3得：所有正有理数组成的集合可数.

又所有负有理数组成的集Q-与Q+一一对应，所以，Q-也是可数的.

然而，全体有理数组成的集合Q=Q+∪Q-∪{0}，因此，Q是可数的.

定理4.7 实数集R不可数.

证明 要证明实数集R不可数，只需证明区间（0，1]中的点不可数.即：只需证明区间（0，1]中的点与正整数之间不存在一一对应关系.在十进制下，0与1之间的每个实数都可以写成0.p1 p2 p3…这种形式的无限小数，并约定将有理数写成无限小数，如1/2=0.499 9….假设实数集（0，1]是可数的，将其元素全部枚举出来，得到序列

于是正整数集与实数集（0，1]之间可构成一一对应：

现在构造一个数b=0.b1b2…bi…，其中

则b是0与1之间的其数字都是4或5的一个无限小数，并且它的第i位数字bi≠pii，所以b与（1）式中的任何一个数都不相等.这就是说，数列（1）并没有把（0，1]中的数枚举完.因此，假设（0，1]可数是错误的.故区间（0，1]不可数.

需要注意：①在上述证明中，康托尔在构造数b时，那里的数字4和5并不起什么特殊的作用，只使用了b的一种性质，即：b的第i位数字bi与（1）式中的第i个数的第i位数字pii不同.其实，与pii不同的其余九个数字都可以作为bi.在证明中起决定作用的是对角线上的数字pii.这种证明方法称为康托尔对角线法或者否定型的对角线法.②上述论证过程，也可以用集合论的语言来描述.假设（0，1]中的实数可数，不妨假设

（0，1]={a1，a2，a3，…，an，…}，

其中：ai=0.pi1 pi2…pij…，pij∈{0，1，2，…，9}，i，j∈N.

现在，分别构造集合A和数b如下：

A={a|a=0.a1 a2…ai…∧ai≠pii∧0≤ai≤9∧i∈N}，

b=0.b1b2b3…bi…∧i∈N∧0≤bi≤9.

于是，b∈A当且仅当bi≠pii（i∈N）.

因此，A≠∅并且A⊆（0，1]，但A≠（0，1].因为b是A不等于（0，1]中任意数的一个证据.所以，所有（0，1]中的数可以排列成a1，a2，…，an，…的假设是错误的.故（0，1]中的实数不可数.③为什么人们把上面的论证方法叫做对角线方法呢？这是因为直线y=x在二维直角坐标系中代表一、三象限的对角线，而有序对〈x，x〉（x∈R）在二维直角坐标系中是直线y=x上的点.因此，对任意的x∈R，〈x，x〉就是一、三象限的对角线上的点.按照这种分析，我们可以把（2）式中的实数写成如下的形式：

因此，pii所在的位置可以记作〈i，i〉.pij所在的位置记作〈i，j〉（当i≠j时），bi（i=1，2，…）是0～9之间的数并且不等于对角线上的元素pii.

根据上面的分析，我们可以总结出采用对角线方法证明问题的步骤.第一步：枚举.把我们要处理的对象（比如：自然数、集合、函数等）枚举出来.如前面的枚举：

a1，a2，a3，…，an，….

第二步：按照一定的关系列出一边是枚举对象，另一边是相关的对象而得到的坐标系.第三步：在坐标系的对角线位置上取否定而得到所需要的东西，即上面的数b.

定义4.9 设有两个集合A和B.如果存在一个从A到B的双射f，那么称A和B等势，记作，并称A与B是一一对应的.

例4.8 设A={a，b，c}，B={1，2，3}，则.因为设f={〈a，1〉，〈b，2〉，〈c，3〉}，则f是A到B的一个双射，所以.此处f是A与B之间的一个一一对应.除f之外，A与B之间还存在其他双射.例如，f′={〈a，1〉，〈b，3〉，〈c，2〉}，显然，f′也是A到B的一个双射.所以，A与B之间的一一对应不是唯一的.

例4.9 令X={1，2，3，…，n，…}，Y={1，4，9，…，n2，…}，则事实上，显然f（n）=n2是从集合X到集合Y的一个双射，故如下所示：

例4.9回答了伽利略的问题.同时也说明，正整数集合能与它的一个真子集一一对应.这也是无限集的一个特点.

定义4.10 如果集合A与集合B的一个真子集能构成一一对应，但B与A的任一真子集都不能构成一一对应，那么我们说A的势小于B的势，记作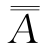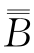＜.当存在A到B的单射时，我们只能说A的势不大于B的势，记作

对于有限集合来说，势就是它所包含的元素的数目，并且当A是B的真子集时，根据“整体大于部分”这一原则，必有但是对无限集合来说，这一原则失效.要想比较两个无限集所含元素的“多少”，就必须利用势的概念.

集合之间的等势关系满足等价关系的条件.即，等势具有下面的性质：

（1）

（2）如果，则

（3）如果并且，则

这些性质的证明留作练习.

最后，我们以康托尔定理来结束本章的讨论.

定理4.8 （康托尔定理，1891） 对于任一集合A，都有

证明 分两步来证明它.第一步证明，第二步证明

第一步：对于任一x∈A，令f（x）={x}.当x1≠x2时，有{x1}≠{x2}，即f（x1）≠f（x2）.所以f是A到P（A）的一个单射函数.因此

第二步：用反证法.假定，则必存在一双射函数g：A→P（A），对于任一x∈A，g（x）∈P（A），即g（x）⊆A.现在我们考察这一x是否属于g（x）.其实，x可能属于g（x），也可能不属于g（x）.令

显然A0⊆A.因为g是双射函数，所以在A中必有一元素y使得g（y）=A0.我们要问：y∈A0吗？若y∈A0，由（*）可得y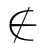g（y）.但是，由y的定义，A0=g（y），所以，得yA0.若y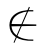A0，由A0=g（y），可得yg（y）.但由（*）可得y∈A0.不论y是否属于A0，都将导致矛盾.因此，这样的双射函数g不存在，故