定义3.11 设R是非空集合X上的一个二元关系.如果R具有自返性、对称性和传递性，那么称R是X上的一个等价关系.习惯上，人们将等价关系R记成～，还将〈x，y〉∈～记成x～y.

例3.12 设A为生活在地球上所有人的集合，则

R={〈x，y〉|x，y∈A并且x与y生活在同一个国家}

是A上的一个等价关系.因为R具有：自返性、对称性和传递性.

例3.13 令X={1，2，3，4，5，6，7，8，9，10}，R={〈x，y〉|x，y∈X并且xy≡0（mod3）}，则R是X上的一个等价关系.因为，x-y≡0（mod3）等价于xy=3m（m是整数），于是，

（1）对任意的x∈X，因为x-x=0=3·0，所以，x-x≡0（mod3），故R在X上是自返的.

（2）对任意的x，y∈X，如果x-y≡0（mod3），即：x-y=3m，亦即：y-x=3·（-m），所以，y-x≡0（mod3），故R在X上是对称的.

（3）对任意的x，y，z∈X，如果x-y≡0（mod3）并且y-z≡0（mod3），即：x-y=3m1并且y-z=3m2，于是，x-z=x-y+y-z=（x-y）+（y-z）=3m1+3m2=3（m1+m2），所以，x-z≡0（mod3），故R在X上是传递的.

定义3.12 设～是非空集合X上的一个等价关系.对任意的x∈X，令[x]～={y|y∈X并且x～y}，则称[x]～为x（关于～）的等价类.

例3.14 例3.12中所有的等价类为世界上的所有国家.即：所有生活在美国的人构成一个等价类，所有生活在法国的人构成一个等价类，所有生活在中国的人构成一个等价类……

例3.15 例3.13中的等价类为：

[1]R=[4]R=[7]R=[10]R={1，4，7，10}，

[2]R=[5]R=[8]R={2，5，8}，[3]R=[6]R=[9]R={3，6，9}.

X中各元素的等价类如图1-11所示.

图1-11

关于等价类有下面的一些结论：

（1）对于任意的x∈X，[x]R≠∅；

（2）若〈x，y〉∈R，则[x]R=[y]R；

（3）若〈x，y〉R，则[x]R∩[y]R=∅；

（4）∪{[x]R|x∈X}=X.

这里的R是X上的一个等价关系.

事实上，对于（1），设任意的x∈X，因为〈x，x〉∈R成立，所以x∈[x]R，故[x]R≠∅.对于（2），设任意的z，z∈[x]R，则〈x，z〉∈R.因为〈x，y〉∈R并且R是X上对称的和传递的关系，于是〈y，x〉∈R并且〈x，z〉∈R，因此〈y，z〉∈R，即z∈[y]R，所以[x]R⊆[y]R.同理可证：[y]R⊆[x]R.故[x]R=[y]R.对于（3），用反证法.假定[x]R∩[y]R≠∅，必存在z0，使得z0∈[x]R并且z0∈[y]R.于是有〈x，z0〉∈R并且〈y，z0〉∈R.由R的对称性和传递性可得〈x，y〉∈R，这与〈x，y〉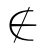R矛盾，故[x]R∩[y]R=∅.对于（4），设任意的z，z∈∪{[x]R|x∈X}，必存在y∈X，使得z∈[y]R.但是，[y]R⊆X，所以z∈X，因而∪{[x]R|x∈X}⊆X.反之，对任意的z，z∈X，〈z，z〉∈R成立，所以z∈[z]R.而[z]R⊆∪{[x]R|x∈X}，因此z∈∪{[x]R|x∈X}.这说明X⊆∪{[x]R|x∈X}.故∪{[x]R|x∈X}=X.

定义3.13 设R是非空集合X上的等价关系，以R的全体等价类为元素的集合称为R的商集，记作X/R或X/～.

由例3.15中的等价类做成的商集为：

X/R={[1]R，[2]R，[3]R}.

定义3.14 设X为一非空集合.如果X的一个子集族A满足：

（1）任给T∈A，都有T≠∅；

（2）任给S，T∈A，S≠T蕴涵S∩T=∅；(www.daowen.com)

（3）∪A=X，那么称A为X上的一个划分，A中的每一个元素称为X的一个划分块.

集合的划分与等价关系之间有非常密切的联系.根据等价类的性质，由X上的等价关系R所决定的等价类恰好是X上的一个划分，并且此划分中的划分块恰好是X中所有元素形成的不同的等价类.反之，若集合X有一划分A={A1，A2，…，An}，定义R为：对任意的x，y∈X，〈x，y〉∈R当且仅当x，y在同一划分块中，即：x，y∈Ai（i=1，2，…，n）.不难证明，R是一个等价关系.因此，一个集合上的划分也确定集合元素之间的一个等价关系.

定义3.15 设R是集合X上的一个二元关系.如果R具有自返性、反对称性和传递性，那么称R为X上的一个偏序关系，简称偏序.习惯上，常将X上的偏序关系R记作≤，而将〈x，y〉∈R记作x≤y.

例3.16 设X为任意集合，R为X的幂集上的包含关系，即

R={〈x，y〉|x，y∈P（X）并且x⊆y}，

可以证明R在P（X）上具有自返性、反对称性和传递性，因此R是P（X）上的一个偏序关系.

根据偏序关系的特点，我们可以将它的关系图化简，其画法如下：

（1）用结点代表元素；

（2）若x≤y并且x≠y，则将代表y的结点画在代表x的结点之上，并且：①若不存在z，使得z≠x并且z≠y并且x≤z≤y，则在x和y之间连线；②若存在z，当z≠x并且z≠y并且x≤z≤y时，则在x和y之间不连线.

这种简化的偏序图称为哈斯（Hass）图.

例3.17 集合X={1，2，3，4，5}，偏序关系为≤（小于等于），其哈斯图如图1-12所示.

图1-12

例3.18 集合X={1，2，3，4，5，6，7，8，9，10，11，12}，偏序关系为整除关系|，其哈斯图如图1-13所示.

图1-13

例3.19 集合X=P（{1，2，3}），偏序关系为⊆（包含关系），其哈斯图如图1-14所示.

图1-14

在例3.18中，元素5和7之间，9和11之间等等，不能比较大小或排序.但在例3.17中，所有元素之间都能比较大小或排序.因此，它的特点是：对应的哈斯图是一条直线.为此，我们有：

定义3.16 设≤为集合X上的一个偏序关系.若对于任意的x，y∈X，均蕴涵x≤y或y≤x，则称≤为X上的全序关系（或线序关系）.

例3.20 自然数集N、整数集Z、有理数集Q和实数集R上的小于等于或大于等于关系都是全序关系.例3.18和例3.19中的偏序关系都不是全序关系.从这些例子可以看出，全序关系的哈斯图是一条直线.凡哈斯图不能表示成直线的偏序关系都不是全序关系.

在集合论中，还有一种常用的偏序关系：

定义3.17 集合X上的关系R若具有反自返性和传递性，则称R为X上的一个严格偏序，记作＜.

例3.21 自然数集N、整数Z、有理数集Q和实数集R上的小于关系，集合之间的真包含关系⊂等等，都是严格偏序关系.

严格偏序关系和偏序关系之间有密切的联系.如果＜是一个严格偏序关系，那么相应的偏序关系就可以定义为：x≤y当且仅当x＜y或者x=y.反之，如果≤是一个偏序关系，与此相应的严格偏序关系就可以定义为：x＜y当且仅当x≤y并且x≠y.

另外，集合X上的严格偏序关系＜必是反对称的.事实上，如果＜不是反对称的，则存在x∈X和y∈X使得x＜y并且y＜x.因为＜是一个严格偏序，所以＜必具有传递性.由x＜y并且y＜x可得x＜x.这与＜是反自返的相矛盾.