下面给出的是我们经常考虑的几种特殊的二元关系.

定义3.8 设X是任意的集合，R为集合X上的一个二元关系.若对于任意的x∈X，都有〈x，x〉∈R，则称R为X上的自返关系，或称R具有自返性.若对任意的x∈X，都有〈x，x〉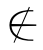R，则称R为X上的反自返关系，或称R具有反自返性.

例3.8 设A为某班全体学生的集合，若

R1={〈x，y〉|x，y∈A并且x与y同性别}，

则R1是A上的自返关系.若

R2={〈x，y〉|x，y∈A并且x比y年龄小}，

则R2是A上的反自返关系.

自返性是说X中的每个元素自己和自己有R关系，反自返性是说X中的所有元素自己和自己没有R关系.

定义3.9 设X是任意集合，R是集合X上的一个二元关系.对于任意的x∈X，y∈X，（1）若〈x，y〉∈R蕴涵〈y，x〉∈R，则称R为X上的对称关系，或称R具有对称性；（2）若〈x，y〉∈R并且〈y，x〉∈R蕴涵x=y，则称R为X上的反对称关系，或称R具有反对称性.

例3.9 兄弟关系、同学关系、朋友关系都是对称关系，但不是反对称关系.

例3.10 设R1={〈0，0〉，〈1，1〉，〈2，2〉，〈3，3〉，〈0，1〉，〈0，2〉，〈0，3〉，〈1，0〉，〈2，0〉，〈3，0〉}，则R1是A={0，1，2，3}上的对称关系.而R2={〈0，0〉，〈1，1〉，〈2，2〉，〈3，3〉}是A上的反对称关系.除此之外，R1和R2还是A上的自返关系.

对称性要求，若X中的任意两个元素x和y之间有R关系，则y和x之间也有R关系.反对称性要求，若X中的任意两个元素之间按不同顺序都有R关系，则这两个元素一定相等.

定义3.10 设X是任意的集合，R是集合X上的一个二元关系.对任意的x∈X，y∈X，z∈X，如果〈x，y〉∈R并且〈y，z〉∈R蕴涵〈x，z〉∈R，那么称R是X上的传递关系，或称R具有传递性.(www.daowen.com)

例3.11 自然数集N上的小于关系和小于等于关系都具有传递性，亲兄弟关系也具有传递性，但是同学关系和父子关系都不具有传递性.

以上五种关系或性质，都可以用集合的运算来表示.设A是任意的集合，R⊆A×A，则这些关系或性质用集合的运算可分别表示如下：

（1）自返性 IA⊆R；

（2）反自返性 IA∩R=∅；

（3）对称性 R=R-1；

（4）反对称性 R∩R-1⊆IA；

（5）传递性 R◦R⊆R.

关于（1）的证明：事实上，只需证R是A上的自返关系，当且仅当IA⊆R.对任意的x∈A，〈x，x〉∈IA，因为R是自返的，根据定义3.8得：〈x，x〉∈R.于是，IA⊆R.反之，对任意的x∈A，因为〈x，x〉∈IA并且IA⊆R，由定义1.3得：〈x，x〉∈R.再由定义3.8得：R是自返的.

关于（2）的证明：事实上，只需证R是A上反自返的当且仅当IA∩R=∅.假设IA∩R≠∅，即：任意的x∈A，〈x，x〉∈IA∩R，根据定义2.2得：〈x，x〉∈IA且〈x，x〉∈R，这与R是反自返的矛盾.反之，因为IA∩R=∅，所以，对任意的x∈A，因为〈x，x〉∈IA，所以，〈x，x〉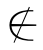R.根据定义3.8得，R是反自返的.

关于（3）的证明：事实上，只需证R是A上对称的二元关系当且仅当R=R-1.对任意的x，y∈A，假设〈x，y〉∈R，因为R是对称的，由定义3.9得：〈y，x〉∈R.根据定义3.7的（6）得：〈x，y〉∈R-1.于是，R⊆R-1.假设〈x，y〉∈R-1，根据定义3.7的（6）得：〈y，x〉∈R，又R是对称的，则〈x，y〉∈R.于是，R-1⊆R.综上所述，得R=R-1.反之，对任意的x，y∈A，假设〈x，y〉∈R，因为R=R-1，所以，〈x，y〉∈R-1，根据定义3.7的（6）得：〈y，x〉∈R.根据定义3.9可得：R是对称的.

关于（4）的证明：事实上，只需证R是A上的反对称关系当且仅当R∩R-1⊆IA.对任意的x，y∈A，假设〈x，y〉∈R∩R-1，由定义2.2，〈x，y〉∈R且〈x，y〉∈R-1.由定义3.7的（6）可得：〈y，x〉∈R.再由定义3.9可得：x=y，即〈x，x〉∈R∩R-1，又〈x，x〉∈IA，即〈x，y〉∈IA，所以，R∩R-1⊆IA.反之，因为R∩R-1⊆IA，所以，由〈x，y〉∈R∩R-1，可得〈x，y〉∈IA.根据定义3.7的（2）可得：x=y.又因为〈x，y〉∈R∩R-1，根据定义2.2可得：〈x，y〉∈R且〈x，y〉∈R-1，由定义3.7的（6）可得：〈y，x〉∈R.由定义3.9可得：R是反对称的.

关于（5）的证明：事实上，只需证R是A上的传递关系当且仅当R◦R⊆R.对任意的x，y∈A，假设〈x，y〉∈R◦R，根据定义3.7的（7）可得：存在z∈A使得：〈x，z〉∈R且〈z，y〉∈R.又R是传递的，则〈x，y〉∈R.反之，设〈x，z〉∈R并且〈z，y〉∈R，由定义3.7的（7）可得：〈x，y〉∈R◦R，又R◦R⊆R，所以，〈x，y〉∈R.故R是传递的.