在日常生活中，关系的例子是很多的.比如父子关系、师生关系和朋友关系等等.数学家也经常研究数学对象之间的关系.两类对象之间的关系出现得最频繁，我们称之为二元关系.例如，如果直线l过点p，我们就说直线l和点p有关系R.也就是说，R就是那个叫直线l的事物和那个叫点p的事物之间的二元关系.与此类似，数之间的小于号“＜”也是一种二元关系.

定义3.4 如果一个集合R上的所有元素都是有序对，那么R就是一个二元关系.即：若任一个z∈R，则存在x和y使得z=〈x，y〉.

习惯上，用x Ry代表〈x，y〉∈R.我们说，如果x Ry成立，x和y就有R关系.

下面是定义3.4的推广.

定义3.5 如果一个集合的全体元素为n（＞1）元有序组，那么称这个集合为一个n元关系.记作Rn.特别地，对于空集，我们称它为空关系.

二元关系具有下面的性质：

（1）如果R是一个二元关系，并且S⊆R，则S也是一个二元关系；

（2）如果R和S都是二元关系，则R∩S，R∪S，R-S也是二元关系.

事实上，对于性质（1），因为R是一个二元关系，由定义3.4得：R的全体元素为二元有序对.又因S⊆R，所以，S的全体元素也是一个二元有序对.再利用定义3.4可得：S是一个二元关系.

对于性质（2），对任意的a，a∈R∩S，由定义2.2得：a∈R并且a∈S.因为R和S都是二元关系，所以a是二元有序对，故：R∩S是一个二元关系.同理可证：R∪S和R-S也都是二元关系.

例3.6 关系R是集合{z|存在正整数m和n，使得z=〈m，n〉并且m可以整除n}.因此，R的元素都是如下的有序对：

〈1，1〉，〈1，2〉，〈1，3〉，…

〈2，2〉，〈2，4〉，〈2，6〉，…

〈3，3〉，〈3，6〉，〈3，9〉，…

定义3.6 设有两个集合A和B，由A×B的任意子集所确定的一个二元关系称为集合A到B上的一个二元关系.特别地，当B=A时，则称A×A的任意子集为集合A到集合A上的一个二元关系，或称A上的一个二元关系.

定义3.7 设R⊆A×A，T⊆A×A，B⊆A，称

（1）{〈x，y〉|x∈A并且y∈A}为A上的全域关系，记作EA；

（2）{〈x，x〉|x∈A}为A上的恒等关系，记作IA；

（3）{x|存在y，使得〈x，y〉∈R}为R的定义域，记作dom（R）；

（4）{y|存在x，使得〈x，y〉∈R}为R的值域，记作ran（R）；

（5）dom（R）∪ran（R）为R的域，记作fld（R）；

（6）{〈y，x〉|〈x，y〉∈R}为R的逆，记作R-1；(www.daowen.com)

（7）{〈x，y〉|存在z，使得〈x，z〉∈R并且〈z，y〉∈T}为R与T的合成（或复合），记作R◦T.当R=T时，R◦T记作T◦T；

（8）{〈x，y〉|〈x，y〉∈R并且x∈B}为R在B上的限制，记作R↾B；

（9）ran（R↾B）为B在R下的像，记作R[B].

例3.7 令R是例3.6中的一个二元关系，则

dom R={m|存在n使得m整除n}=所有正整数的集合.

ran R={n|存在m使得m整除n}=所有正整数的集合.

fld R=dom R∪ran R=所有正整数的集合.

R-1={z|z=〈n，m〉并且〈m，n〉∈R}

={z|z=〈n，m〉并且m可以整除n}

={z|z=〈n，m〉并且n是m的倍数}.

如果令B={4，7}，则

R↾B={〈4，4〉，〈4，8〉，〈4，12〉，…，〈7，7〉，〈7，14〉，…}，

R[B]={4z|z∈Z+}∪{7z|z∈Z+}.

关系的逆和复合具有下面的性质：

（1）（R1◦R2）◦R3=R1◦（R2◦R3）；

（2）dom（R-1）=ran（R），ran（R-1）=dom（R）；

（3）（R-1）-1=R；

（4）（R1◦R2）-1=◦.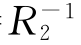

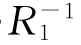关于（R1◦R2）-1=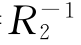◦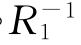的证明如下：

事实上，设〈x，y〉∈（R1◦R2）-1，则〈y，x〉∈R1◦R2.根据关系复合的定义得：存在z，使得〈y，z〉∈R1并且〈z，x〉∈R2.于是，存在z，使得〈x，z〉∈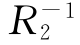并且〈z，y〉∈R-11，由此可得：〈x，y〉∈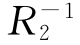◦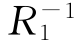，由定义1.3得，（R1◦R2）-1⊆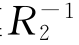◦.同理可证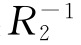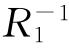：◦⊆（R1◦R2）-1.故：（R1◦R2）-1=◦.

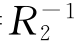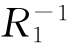其他性质的证明，留给读者练习.