定义3.3 设有两个集合A和B，并且a∈A，b∈B，由所有二元有序对〈a，b〉组成的集合，称为A与B的笛卡儿乘积，记作A×B，读作A叉乘B，即：

A×B={〈a，b〉|a∈A并且b∈B}.

亦即：

x∈A×B当且仅当存在a∈A，存在b∈B，使得x=〈a，b〉.

例3.1 设A={a，b，c，d}，B={a，b}，则

A×B={〈a，a〉，〈a，b〉，〈b，a〉，〈b，b〉，〈c，a〉，〈c，b〉，〈d，a〉，〈d，b〉}，

B×A={〈a，a〉，〈a，b〉，〈a，c〉，〈a，d〉，〈b，a〉，〈b，b〉，〈b，c〉，〈b，d〉}.

例3.2 令A=R（全体实数集），则R×R表示二维的欧几里得平面，〈2，4〉∈R×R是平面上的一点.

例3.3 设A={x|0≤x≤2}，B={y|0≤y≤3}，则

A×B={〈x，y〉|0≤x≤2，0≤y≤3}.

它表示平面直角坐标系x Oy中所示的矩形区域，如图1-10中的阴影部分.

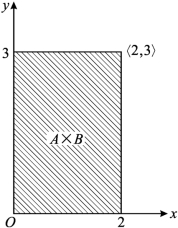
图1-10

类似地，可以定义三个集合和n个集合的笛卡儿乘积.

A×B×C={〈x，y，z〉|x∈A并且y∈B并且z∈C}，

A1×A2×…×An={〈x1，x2，…，xn〉|xi∈Ai，i=1，2，…，n}.

例3.4 设A={2，3}，B={4}，C={1，0}，则

A×B×C={〈2，4，1〉，〈2，4，0〉，〈3，4，1〉，〈3，4，0〉}.

例3.5 设R是实数集，则R×R×R表示三维欧几里得空间，〈x，y，z〉∈R×R×R是空间中的任一点，其中x，y，z∈R.(www.daowen.com)

笛卡儿乘积具有下面的性质：

（1）A×B=∅当且仅当A=∅或B=∅；

（2）A×B=B×A当且仅当A=∅或B=∅或A=B；

（3）若A≠∅且A×B⊆A×C，则B⊆C；

（4）若B⊆C，则A×B⊆A×C；

（5）笛卡儿乘积的四种形式的分配律：

A×（B∩C）=（A×B）∩（A×C），

（B∩C）×A=（B×A）∩（C×A），

A×（B∪C）=（A×B）∪（A×C），

（B∪C）×A=（B×A）∪（C×A）.

（6）如果A⊆C并且B⊆D，则A×B⊆C×D.

下面仅给出性质（1）～（3）和笛卡儿乘积对交的分配律的证明，其他证明留作练习.

事实上，对于性质（1），如果A≠∅并且B≠∅，那么就存在a∈A，b∈B，使得〈a，b〉∈A×B，这与A×B=∅矛盾，故A=∅或B=∅.反之，如果A×B≠∅，则存在a∈A，b∈B使得〈a，b〉∈A×B.于是，有A≠∅并且B≠∅矛盾，故A×B=∅.

对于性质（2），如果A×B=B×A时，A=∅或B=∅或A=B不成立.即：A≠∅并且B≠∅并且A≠B成立，那么存在a∈A并且b∈B.又因A≠B，不妨设a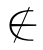B.于是，由〈a，b〉∈A×B，可得〈a，b〉∈B×A.即：a∈B，这与假设a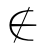B矛盾.反之，①当A=B时，结论显然成立；②如果A=∅或B=∅，则A×B=B×A=∅，结论成立.

对于性质（3），设b∈B，因为A≠∅，不妨设a∈A.于是〈a，b〉∈A×B，又A×B⊆A×C，所以，〈a，b〉∈A×C，故b∈C，即：B⊆C.

关于A×（B∩C）=（A×B）∩（A×C）的证明：

如果〈x，y〉∈A×（B∩C），由定义3.3得：x∈A并且y∈（B∩C），即：x∈A并且（y∈B并且y∈C）.亦即：（x∈A并且y∈B）并且（x∈A并且y∈C），再由定义3.3得：〈x，y〉∈A×B并且〈x，y〉∈A×C，所以〈x，y〉∈（A×B）∩（A×C）.由此可得：A×（B∩C）⊆（A×B）∩（A×C）.同理可证：（A×B）∩（A×C）⊆A×（B∩C）.故：A×（B∩C）=（A×B）∩（A×C）.