设E相对于集合A，B和C是全集，A，B和C为E的任意子集，则集合的运算具有下面的性质：

（1）幂等律 A∪A=A，A∩A=A；

（2）结合律 （A∪B）∪C=A∪（B∪C），

（A∩B）∩C=A∩（B∩C）；

（3）交换律 A∪B=B∪A，A∩B=B∩A；

（4）分配律 A∪（B∩C）=（A∪B）∩（A∪C），

A∩（B∪C）=（A∩B）∪（A∩C）；

（5）空集律 A∪∅=A，A∩∅=∅；

（6）全集吸收律 A∪E=E，A∩E=A；

（7）排中律 A′∪A=A∪A′=E；

（8）矛盾律 A∩A′=A′∩A=∅；

（9）吸收律 A∪（A∩B）=A，A∩（A∪B）=A；

（10）德·摩根律 （A∪B）′=A′∩B′，（A∩B）′=A′∪B′；

（11）余补律 ∅′=E，E′=∅；

（12）双重否定律 （A′）′=A.(www.daowen.com)

下面给出交的结合律、交换律和德·摩根律的证明.

（1）关于（A∩B）∩C=A∩（B∩C）的证明如下：

由定义2.2，对任意的x，x∈（A∩B）∩C，则x∈A∩B并且x∈C.由此可得：（x∈A并且x∈B）并且x∈C.由此可得：x∈A并且（x∈B并且x∈C）.由定义2.2可得：x∈A并且x∈B∩C.再利用定义2.2得：x∈A∩（B∩C）.因此，（A∩B）∩C⊆A∩（B∩C）.同理可证：A∩（B∩C）⊆（A∩B）∩C.故：（A∩B）∩C=A∩（B∩C）.

说明交的结合律成立的文氏图见图1-8.

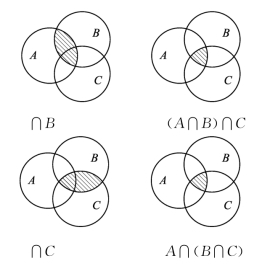
图1-8

（2）关于A∩B=B∩A的证明如下：

由定义2.2，对任意的x，x∈A∩B，则x∈A并且x∈B.由此得：x∈B并且x∈A.再由定义2.2得：x∈B∩A.因此，A∩B⊆B∩A.同理可证：B∩A⊆A∩B.故：A∩B=B∩A.

（3）关于（A∪B）′=A′∩B′的证明如下：

由定义2.5，如果x∈（A∪B）′，则xA∪B，即xA并且xB，亦即x∈A′并且x∈B′，因此x∈A′∩B′，所以（A∪B）′⊆A′∩B′.反之，如果x∈A′∩B′，由定义2.2得，x∈A′并且x∈B′.利用定义2.5得：xA并且xB，所以x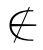A∪B，再由定义2.5得：x∈（A∪B）′，于是A′∩B′⊆（A∪B）′.综前所述：（A∪B）′=A′∩B′.

说明并的德·摩根律成立的文氏图见图1-9.

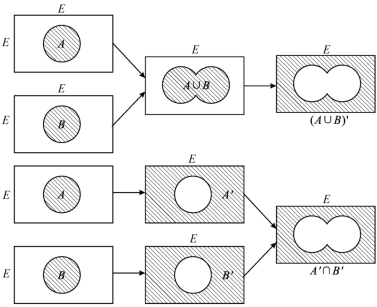
图1-9

其他算律的证明，留给读者练习.