定义2.4 设有两个集合A和B，由属于A而不属于B的全体元素组成的集合称为A与B的差集，记作A-B，读作A减B.符号“-”表示两个集合之间差的运算.如图1-6的阴影部分的区域表示A-B，即：

图1-6

A-B={x|x∈A并且x/∈B}.

亦即：

x∈A-B当且仅当x∈A并且xB.

例2.6 当A={a，b}，B={a，b，c，d}，C={a，c，e}时，B-A={c，d}，A-B=∅，A-C={b}，C-A={c，e}.

差集具有下面的性质：

（1）A-（B∪C）=（A-B）∩（A-C）；

（2）A-（B∩C）=（A-B）∪（A-C）.

事实上，对于性质（1）只需证明：A-（B∪C）⊆（A-B）∩（A-C）并且（AB）∩（A-C）⊆A-（B∪C）.对任意的x，x∈A-（B∪C），根据定义2.4可得：x∈A并且x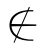B∪C.由x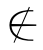B∪C可得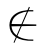：xB并且x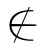C.于是，有x∈A并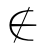且（xB并且xC）.由此可得：（x∈A并且xB）并且（x∈A并且xC）.再根据定义2.4可得：x∈A-B并且x∈A-C.利用定义2.2得：x∈（A-B）∩（AC）.于是A-（B∪C）⊆（A-B）∩（A-C）；反之，对任意的x，x∈（A-B）∩（A-C），根据定义2.2可得：x∈A-B并且x∈A-C.由定义2.4可得：（x∈A并且xB）并且（x∈A并且xC）.由此可得：x∈A并且（xB并且xC）.利用定义2.1得：x∈A并且xB∪C，再利用定义2.4可得：x∈A-（B∪C）.于是，（A-B）∩（A-C）⊆A-（B∪C）.综前所述得：A-（B∪C）=（A-B）∩（A-C）.同理可证性质（2）成立.

定义2.5 若B⊆A，则A-B叫做B对A的相对补.记作B′，读作B的补.符号“′”表示集合的补运算.如图1-7的阴影部分的区域表示B′，即：

图1-7

B′={x|x∈A并且xB}.

亦即，若B⊆A，x∈B′当且仅当x∈A且xB.

特别地，差和相对补之间满足下面的等式：(www.daowen.com)

A-B=A∩B′.

例2.7 当A={a，b}，B={a，b，c，d}时，A′=B-A={c，d}.而A-B=∅.

相对补具有下面的性质：

（1）（A′）′=A；

（2）（A∩B）′=A′∪B′，（A∪B）′=A′∩B′.

事实上，性质（1）只需证明：（A′）′⊆A并且A⊆（A′）′.对于任意的x，x∈（A′）′，根据定义2.5，xA′，再利用定义2.5，得：x∈A.于是，（A′）′⊆A.反之，对任意的x，x∈A，则xA′.由定义2.5得：x∈（A′）′.于是，A⊆（A′）′.综前所述，得：（A′）′=A.对于性质（2），只证等式（A∩B）′=A′∪B′成立.对任意的x，x∈（A∩B）′，根据定义2.5得：x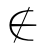A∩B，即xA或者x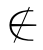B.再利用定义2.5得：x∈A′或x∈B′.于是，x∈A′∪B′.即：（A∩B）′⊆A′∪B′.同理可证：A′∪B′⊆（A∩B）′.剩下的证明留给读者完成.

利用集合的并运算，我们有：

定义2.6 一个集合A的后继集A+如下：

A+=A∪{A}.

利用后继运算，冯·诺伊曼提出了一种刻画自然数的办法.他把每个自然数都定义为如下较小自然数的集合.

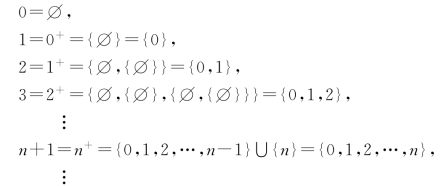
这样构造出来的自然数具有下面的两条性质：

0∈1∈2∈3∈…∈n∈（n+1）∈…，

0⊆1⊆2⊆3⊆…⊆n⊆（n+1）⊆….

并且自然数集N为：

{0，1，2，3，…，n，n+1，…}={∅，∅+，∅++，…，∅++…+，…}.