定义2.1 设有两个集合A和B，由A和B的所有元素构成的集合称为集合A与集合B的并集，记作A∪B，读作A并B.符号“∪”表示两个集合之间的并运算.如图1-4的阴影部分的区域表示A∪B.即：

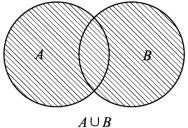
图1-4

A∪B={x|x∈A或者x∈B}，

亦即：

x∈A∪B当且仅当x∈A或者x∈B.

例2.1 令A={a，b}，B={a，b，c，d}，C={a，c，e}，则A∪B={a，b，c，d}，A∪C={a，b，c，e}，B∪C={a，b，c，d，e}.

例2.2 令A={3个苹果}={a1，a2，a3}，B={2个苹果和3个梨}={a4，a5，b1，b2，b3}，则A∪B={a1，a2，a3，a4，a5，b1，b2，b3}.即：集合A∪B中有8个元素，其中5个苹果和3个梨.

从例2.2可以看出，两个集合并的运算可以看作算术加法的一种推广.因为数的加法要求名数相同的量才能相加.集合的并运算不仅能使同名数的量能相加，而且也较好地处理了不同名数量的计算.就是说，不同名数两个集合并的结果，等于一个新的集合.这个集合中，元素的个数等于两个集合中元素个数的和，而集合中元素之间又是可以相互区分的.

用类似的方法可以定义两个以上集合的并集.设A1，A2，…，An是n个集合，则

A1∪A2∪A3={x|x∈A1或x∈A2或x∈A3}，

A1∪A2∪…∪An={x|x∈A1或x∈A2或…或x∈An}

我们还可以定义集合族A={A|A是集合}的并∪A为：

∪A={x|存在A∈A，使x∈A}.

特别地，当A={Ai|i∈N}时，(www.daowen.com)

当A={Ai|0≤i≤n}={A0，A1，…，An}时，

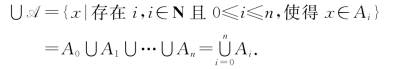
例2.3 当集合族A={{1，2}，{2}，{2，3}}时，∪A={1，2}∪{2}∪{2，3}={1，2，3}.

集合的并具有下面的性质：

（1）交换律 A∪B=B∪A；

（2）结合律 （A∪B）∪C=A∪（B∪C）；

（3）幂等律 A∪A=A；

（4）空集律 A∪∅=A；

（5）A⊆A∪B，B⊆A∪B；

（6）A⊆B当且仅当A∪B=B；

（7）A⊆C并且B⊆C当且仅当A∪B⊆C.

事实上，对于性质（1）只需证明：A∪B⊆B∪A并且B∪A⊆A∪B.因为对于任意的x，x∈A∪B，根据定义2.1可得：x∈A或者x∈B.于是，有x∈B或者x∈A.再根据定义2.1可得：x∈B∪A.因此，A∪B⊆B∪A.同理可证：B∪A⊆A∪B.故A∪B=B∪A.对于性质（2）只需证明：（A∪B）∪C⊆A∪（B∪C）并且A∪（B∪C）⊆（A∪B）∪C.因为对任意的x，x∈（A∪B）∪C，根据定义2.1可得，x∈A∪B或x∈C，再利用定义2.1得：（x∈A或x∈B）或x∈C，由此得：x∈A或（x∈B或x∈C）.于是，有x∈A或x∈B∪C，进一步可得：x∈A∪（B∪C）.因此，（A∪B）∪C⊆A∪（B∪C）.同理可证：A∪（B∪C）⊆（A∪B）∪C.综前所述：（A∪B）∪C=A∪（B∪C）.

对于性质（3）只需注意：x∈A或者x∈A当且仅当x∈A.对性质（4），因为x∈∅为假，所以，x∈A或者x∈∅当且仅当x∈A.对于性质（5），对任意的x，x∈A，得：x∈A或x∈B.即x∈A∪B.因此，A⊆A∪B.对于性质（6），设x∈A∪B，由定义2.1可得x∈A或者x∈B，因为A⊆B，所以，当x∈A时，x∈B.于是，由x∈A或者x∈B可得x∈B或者x∈B，即x∈B.根据定义1.3可得：A∪B⊆B.利用性质（5）可得：B⊆A∪B.于是，当A⊆B时，可得A∪B=B.反之，对任给的x，x∈A，再由性质（5）得：x∈A∪B.因为A∪B=B，所以x∈B.根据定义1.3得：A⊆B，对性质（7），对任意的x，x∈A∪B，由定义2.1和已知条件可得x∈C.反之，设x∈A，由性质（5）可得x∈A∪B，又A∪B⊆C，所以，x∈C.根据定义1.3可得：A⊆C.同理可证：B⊆C.