定义1.3 如果集合A的每一个元素都是集合B的元素，即“对任意的a，若a∈A，则a∈B”，那么称集合A为集合B的子集，记作A⊆B或者B⊇A，读作A包含于B或者B包含A.符号“⊆”或者“⊇”表示集合之间的包含关系.即：A⊆B当且仅当对任意的a，如果a∈A，则a∈B.图1-2的阴影部分的区域表示A⊆B.否则，如果A中有元素不属于B，即“存在x，x∈A并且x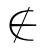B”，则称A不是B的子集.记作A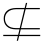B，读作A不包含于B或者B不包含A.如图1-3.

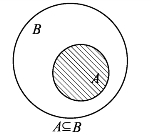
图1-2

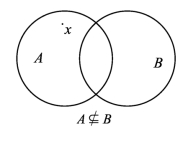
图1-3

例1.6 设A={a，b，c}，B={a，b，c，d}，C={a，b}，则A，B和C三者之间的包含关系为：A⊆B，C⊆A和C⊆B；还有A⊆A，B⊆B和C⊆C（为什么？）.除了这6种包含关系外，A，B和C三者之间再无别的包含关系了.

例1.7 设A={a，{a}，{a，b}}，B={a}，C={{a}}，D={{a}，{a，b}}，则B，C和D都是A的子集.即：B⊆A，C⊆A并且D⊆A.

包含关系具有下面的性质：

（1）A⊆A，即集合A是它自己的子集，换句话说，集合的包含关系具有自返性.因为命题

对任意的x，如果x∈A则x∈A

总成立.

（2）如果A⊆B并且B⊆C，则A⊆C，即集合的包含关系具有传递性.因为，由A⊆B可得

对任意的x，如果x∈A则x∈B.

再由B⊆C可得

对任意的x，如果x∈B则x∈C.(www.daowen.com)

因为所有A中的元素都在B中，而所有B中的元素又都在C中，根据定义1.3可得对任意的x，如果x∈A，则x∈C，即：A⊆C.

定义1.4 设有两个集合A和B，如果A⊆B并且B⊆A，那么称集合A与集合B相等，记作A=B，读作A等于B.符号“=”表示集合之间的相等关系.否则，称集合A不等于集合B，记作A≠B.

例1.8 令X是一个恰好包含数字2，3，5的集合，Y是一个由所有大于1而小于7的素数组成的集合.Z是满足方程x 3-10x 2+31x-30=0的所有解组成的集合.由定义1.4可得：X=Y，X=Z并且Y=Z.这个例子说明，对于同一个集合，我们有不同的描述.

利用集合的包含和相等的概念，我们可以定义真子集和真包含的概念.

定义1.5 设有两个集合A和B，如果A⊆B并且A≠B，那么称集合A是集合B的真子集.记作A⊂B或者AB，读作A真包含于B.

例1.9 在例1.7中，集合B，C和D都是A的真子集.

例1.10 令Z+={x|x∈Z且x＞0}，Q+={x|x∈Q且x＞0}，R+={x|x∈R且x＞0}，分别是正整数集、正有理数集和正实数集，显然，Z+⊂Z，Q+⊂Q，并且R+⊂R，还有：Z+⊂Q+⊂R+.

真包含关系具有下面的性质：

（1）如果A⊂B，则A⊆B；

（2）A⊄A；

（3）如果A⊂B，则B⊄A；

（4）若A⊂B且B⊂C，则A⊂C.

由定义1.5和定义1.3，以上性质是显然成立的.