在逻辑学中，悖论是指这样一个命题α：由α出发，可以找到一个命题β.然后，若假定β，就可以推出非β；若假定非β，就可以推出β.罗素曾构造了这样一个集合，用我们现在使用的符号可以表示为：

也就是说，T是由所有那些不属于自己的集合所组成.现在我们要问：集合T是否属于它自己？

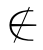倘若假定T∈T，因为T的任何元素x都满足条件xx，所以TT，这与假定T∈T矛盾.反之，倘若假定T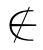T，因为T是由所有那些满足条件xx的x所组成，所以T∈T，这与假定TT矛盾.这个矛盾是罗素1902年发现的集合论悖论，现在简称为罗素悖论.(www.daowen.com)

由于罗素悖论所涉及的概念都是朴素集合论中的基本概念——集合与元素，因而罗素悖论的出现立即震动了整个数学界，引起了数学史上的第三次危机.为了消除悖论，人们开始寻找解决悖论的各种途径和方法.由于当时希尔伯特刚为欧氏几何学成功地建立了公理系统，因此，大家普遍认为采用公理化的方法对集合作一些必要的限制是适当的.1908年，E.策梅洛（Zermelo）给出了第一个集合论公理系统，现在人们称它为Z系统，后经T.斯柯伦（Skolem）、A.弗兰克尔（Frankel）等人的改进，形成了著名的ZF公理系统.然而，ZF系统的展开是形式化的，它是以带等词“=”和隶属关系“∈”的狭谓词演算为基础，加上关于集合基本性质的非逻辑公理组成的形式演绎体系.它的非逻辑公理有：外延公理、空集公理、配对公理、并集公理、幂集公理、子集公理、无穷公理、替换公理、正则公理.如果加上选择公理AC时，得到的系统就是ZFC（ZF+AC）.在ZFC公理系统中，子集公理是一种受到限制的概括原则.用这条公理只能得到与已构造的集合相比并不太大的集合.这样就有效地阻止了悖论的产生，并且还能够得出数学中所需要的东西.除ZF系统以外，还有罗素为解决悖论建立的类型论，冯·诺伊曼（Von Neumann）、P.贝奈斯（Bernays）和K.哥德尔（G¨odel）等人建立的集合论的GB公理系统.有兴趣的读者请参看文献[1].

下面的讨论将是非形式的，因而会出现一些不够严格的情况.形式的讨论，可作为第四章之后的练习.