约定：在本章中，我们用大写字母A，B，C，…，X，Y，Z（或加下标）表示集合或集，用小写字母a，b，c，…，x，y，z（或加下标）表示集合的元素.常用的特殊集合可以用专门的记号表示.如：

例1.4 用N表示全体自然数的集合，用I表示整数集合，用Q表示有理数集合，用R表示实数集合.

定义1.2 如果a是集合A的元素，记作a∈A，读作a属于A；如果a不是集合A的元素，记作a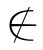A，读作a不属于A.符号∈表示隶属关系.

例1.5 由于N表示全体自然数的集合，所以，0∈N，3∈N，n∈N，但

我们这里所讨论的集合，都具有确定性的特征.也就是说，一个元素是否属于某个集合是可以判定的.“是”或“不是”二者必居其一且只居其一.亦即，对于任意的x和A，x∈A和x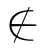A二者必居其一且只居其一.例如，在全体偶数组成的集合中，0，2，4，…都是它的元素，而1，3，5，…都不是它的元素.

一个集合是由它的元素确定的.也就是说，当构成集合的元素给定之后，这个集合也就随之确定.因此，描述一个集合，只要描述它的元素就行了.常用的表示集合的方法有以下两种：

（1）列举法：这种方法是将集合中的全体元素枚举出来，元素之间用逗号隔开，然后用花括号{}括起来.如{真，假}表示由真和假两个元素组成的集合.设A是由最小的4个自然数组成的集合，那么A可以记作{0，1，2，3}.一般地，如果集合A有n个元素a1，a2，…，an，那么记作

A={a1，a2，…，an}.

（2）描述法：设φ（x）表示某个与x有关的性质，A为满足φ（x）的一切x组成的集合，则A可记作

A={x|φ（x）}.

例如，令A表示全体奇数的集合，则A={x|x是奇数}；令B表示由0至2中最小素数的集合，则B={x|x∈N并且0≤x≤2}，即B={2}；令C表示全体偶数的集合，则C={x|x是偶数}或者C={x|x=2n并且n∈N}.(www.daowen.com)

关于集合的表示方法需要注意以下几点：

（1）一个集合中的元素应是互不相同的，因而在集合{a，b}中，a≠b.集合{a，a}仅表示以a为元素的单元集{a}，即{a}就是{a，a}.

（2）集合中的元素不规定顺序，因而{a，b}就是{b，a}.所以，我们习惯上把{a，b}叫做无序对集.

（3）集合的两种表示法有时可以互相转化.这一点我们在前面已经看到.0至2中最小素数的集合既可以表示成{2}，又可以表示成{x|x∈N并且0≤x≤2}.但用性质来刻画集合是最基本的方法.

（4）集合的元素本身还可以是一个集合.如A={1，{1}}，这里1和{1}都是集合A的元素，但{1}本身又是由数1做成的单元素集.又如，B={a，b，{a，b}}.

（5）集合的元素可以是具体的对象，如：{鲁迅、巴金}，{太阳，月亮}；也可以是抽象的，如：{a，b}，{x，y}.甚至在一个集合中，允许一些元素是具体的，另一些元素是抽象的.如：{a，b，鲁迅，巴金}.

（6）全体集合的整体是一个类，不是集合，并规定用V表示.

集合以及集合之间的关系可以用图形表示，这种图形称为文氏（Venn）图.文氏图是用一个简单的平面区域来代表一个集合，如图1-1.集合的元素用区域内的阴影表示.

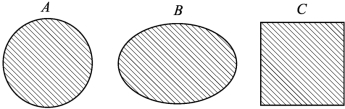
图1-1