海明码是由Richard Hamming在1950年提出的一种具有纠错能力的校验码。海明码是一种多重奇偶校验系统，它的全部码字由原来的数据位和附加的奇偶校验位组成，每一个奇偶位被编在码字的特定位置上，是一种非系统码。海明码能够自动纠正一位错。

生成海明码时的一项基本考虑是确定最少的校验位数k。对于只能纠正一位错的校验码，校验位的位数k和数据位的位数N之间的关系由下面的海明不等式给出：

2^k≥n+k+1

这个公式表明，k个校验位的状态组合应能表示n位数据位哪一位出错、k个校验位哪一位出错和无错这n+k+1种情形。

海明码是由数据位和校验位组成的一种排列，排列方式由海明码的编码规则确定。设k个检验位为P_kP_k-1…P₁，n个数据位为D_nD_n-1D_n-2…D₁，产生的海明码为H_k+nH_k+n-1…H₁，则海明码的编码规则如下。

1）P_i在海明码的第2^i-1位置，即除了最高位，校验位一般放在第1、2、4、8位。数据位则依次从低到高占据海明码中剩下的位置。

2）海明码中的任一位都是由若干校验位来校验的。具体的对应关系如下：被校验的数据位的下标等于所有参与校验该位的校验位的下标之和。而校验位则由自身来检验。一般采用偶校验方法。

海明码的编码规则表明，设计海明码的关键是把每个数据位合理、均匀地分配到相应的校验位中，以确保能发现码字中任何一位出错，并能指出是哪一位出错。实现纠错时，只要对出错位求反就可得到该位的正确值。

现在介绍海明码的编码方法。假设数据位是8位，用D₈D₇D₆D₅D₄D₃D₂D₁表示，根据海明不等式的公式，应安排4位校验位。假设校验位用P₄P₃P₂P₁表示，则生成的海明码具有下列的排列关系，如表3-1所示。

表3-1　海明码的位号等于参与校验该位的校验位的位号之和

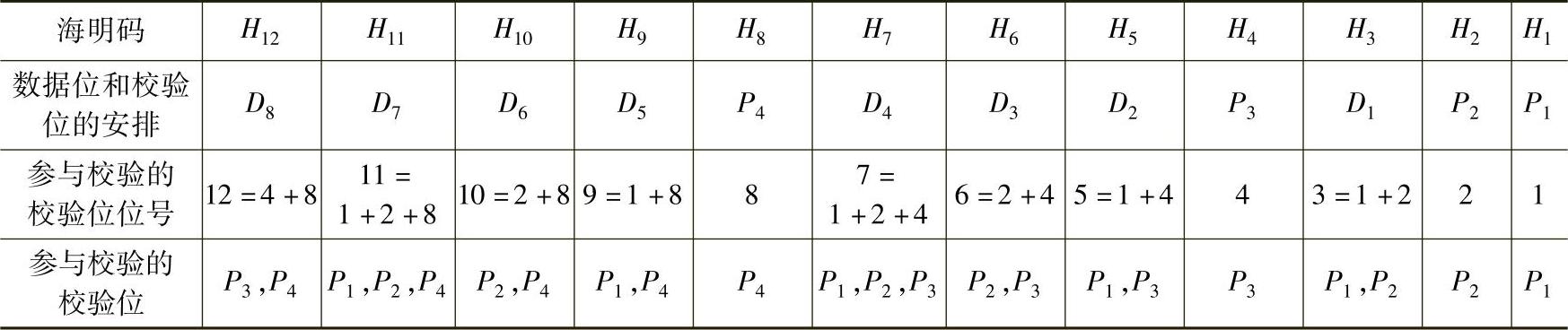
根据校验位与数据位的对应关系表，把每个数据位划分在形成不同校验位的偶校验值的逻辑表达式中。例如，D₈位于H₁₂，12=4+8，P₃的位号是4，P₄的位号是8，即D₈参与P₃和P₄的校验，由此得出海明校验码的编码逻辑表达式如下：

P₁=D₇⊕D₅⊕D₄⊕D₂⊕D₁

P₂=D₇⊕D₆⊕D₄⊕D₃⊕D₁(www.daowen.com)

P₃=D₈⊕D₄⊕D₃⊕D₂

P₄=D₈⊕D₇⊕D₆⊕D₅

例如，如果数据为00110011，把校验位P₄P₃P₂P₁按编码规则插入到数据中：0011P₄001P₃1P₂P₁，根据上式计算出P₄=0，P₃=1，P₂=0，P₁=1，就得到海明码001100011101。

接收时，分别按下式计算S₄S₃S₂S₁，并对S₄S₃S₂S₁进行译码：

S₁=P₁⊕D₇⊕D₅⊕D₄⊕D₂⊕D₁

S₂=P₂⊕D₇⊕D₆⊕D₄⊕D₃⊕D₁

S₃=P₃⊕D₈⊕D₄⊕D₃⊕D₂

S₄=P₄⊕D₈⊕D₇⊕D₆⊕D₅

如果S₄S₃S₂S₁为0000，则表明传输无错，若不是0000，则译码值就是出错的海明码位号。例如，如果S₄S₃S₂S₁=0111，则说明H₇出错，即D₄传输出错。

从上面的表达式中可以看出，不同的数据位出现在P_i项中的次数是不一样的，例如，D₄和D₇出现了3次，而其余的数据位仅出现了2次，当任一个数据位发生变化时，必将引起至少两个P_i值的变化，因此，海明码的码距为3，它可以纠正一位错，或检测2位错。

为了均匀分配数据位，以便平衡对每一个数据位的校验能力，在上面的海明码前再加上一位校验位P₅，P₅的逻辑表达式安排如下：

P₅=D₈⊕D₆⊕D₅⊕D₃⊕D₂⊕D₁

这样，每一位数据位都均匀出现在3个P_i值的形成关系中，当任一个数据位发生变化时，必将引起3个P_i值的变化，因此，这种海明码的码距为4，它可以纠正一位错，并能检测2位错。