SVD分解通过提取兼并线性相关的变量降低空间维数，从而使得某些用多元线性回归难以求解的问题得以用主成分回归求解。sklearn包中提供了decomosition包，并在该包中提供了PCA算法及其很多变种，也是处理降维问题的方案。这些算法的具体应用案例，可以参阅http：//scikit-learn.org/stable/modules/decomposition.html，本节挑选其部分内容讨论。

1.主成分分析PCA

该类对应于传统PCA，与8.1.4节中利用numpy的SVD编写的PCA类一致。使用时在程序中通过下述语句引用：

from sklearn.decomposition import PCA

每个鸢尾花样本用4个变量表述，所以原始空间为4维，样本在空间的分布情况难以直观表达。所以可以选择PCA对其分解，选择前两个主成分组成二维空间实现数据的可视化。

下面的例子分别是利用数据的第1和第3列、PCA前两个主成分作图所得结果。程序代码如下：

程序：鸢尾花主成分投影

程序运行结果如图8.4.5所示，其中8.4.5（a）为原始变量作图结果，8.4.5（b）为PCA作图结果。

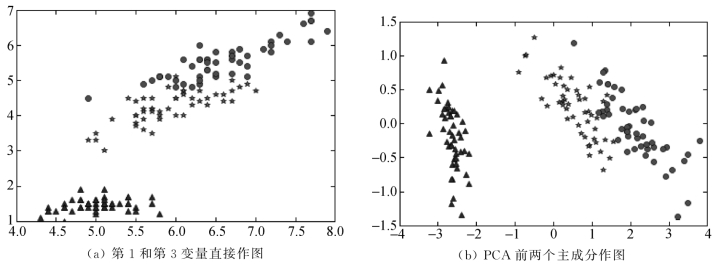
图8.4.5　鸢尾花直接选两变量及PCA降维投影图

2.核PCA(www.daowen.com)

核PCA用类KernelPCA实现。核PCA用于非线性问题的分类，对非线性可分问题，使用KernelPCA可以得到非常好的效果。

下面代码是Mathieu Blondel编写的用于测试KernelPCA的案例。该例是一个非线性可分的问题，使用PCA分解时，由于两类间是包含关系，无法达到分类效果，但使用核PCA，问题得到了很好的解决。程序代码如下：

程序：核PCA

程序的运行结果如图8.4.6所示。

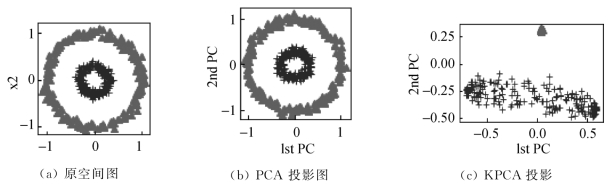
图8.4.6　KPCA分类非线性问题

可以发现，图8.4.6（a）和（b）几乎无差异，即这类包含问题，PCA是难以求解的，但使用KPCA，如图8.4.6（c）所示，可以得到很好的解决。

总之，空间降维在模式分类、建模预测中应用广泛，深入地对其进行理解需要阅读更多的相关理论及研究相关案例。