贝叶斯分类是一类基于概率统计理论进行分类的算法的总称，这类算法均以贝叶斯定理为基础。

贝叶斯定理求解的问题为：已知某条件概率，如何得到两个事件交换后的概率。也就是在已知P（A|B）的情况下，如何求得P（B|A）。条件概率P（A|B）的定义则为：事件B已发生的前提下，事件A发生的概率，称作事件B发生下事件A的条件概率。条件概率的求解公式为：

贝叶斯定理求解P（B|A）公式为：

朴素贝叶斯（Naïve Bayes，NB）分类是贝叶斯分类中的一种，之所以称它为朴素贝叶斯，就是因为它的想法很朴素。现实生活中人们去判断某件事作出结论时，通常以最大概率为准。

以一组简单的数据来描述朴素贝叶斯如何实现分类更能说明问题。设采集了一组外国留学生的简单信息，以肤色作为数据特征，来判断其来源地，得到的信息罗列于表8.4.1。

表8.4.1　朴素贝叶斯分类样本集

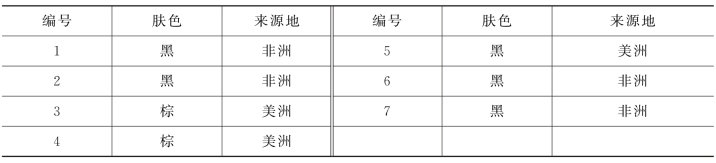
此时，统计来自非洲的学生（即事件B“非洲”发生条件下），事件A“肤色黑”发生的概率为

统计事件B“美洲”发生条件下，事件A“肤色黑”发生的概率P黑|美洲=1/3。现在给定一个事件A“肤色黑”，判断其“来源地”事件B的概率，可以计算如下：

P非洲|黑=P黑|非洲×P非洲/P黑=100%×（样本中非洲的概率）/（样本中肤色黑的概率）

=1×(4/7)/(5/7)=4/5

P美洲|黑=1/3×（样本中美洲的概率）/（样本中肤色黑的概率）

=1/3×(3/7)/(5/7)=1/3×3/5=20%

由此根据大概率原则，可以判断此人来自非洲。

上述例子中对象的特征是非连续值，如“黑”可用1表达，“棕”用2表达，因而很容易计算其出现的概率。实际科学计算问题中，对象特征常常是连续的数值。在这种情况下，贝叶斯认为样本服从正态分布，因而可以使用正态分布计算其概率，公式如下：

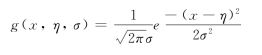
其中x是样本集，σ为方差，η为均值。

对训练集中样本分类ci，对象特征ak的条件概率可根据下式计算：

从而使得贝叶斯算法容易实施。(www.daowen.com)

在很多情况下，朴素贝叶斯分类算法可以与决策树和神经网络分类算法相媲美，且方法简单、分类准确率高、速度快。

Sklearn的naive_bayes包中含有朴素贝叶斯，使用过程也被sklearn统一了调用格式，与前面提到的支持向量机调用格式类似。使用朴素贝叶斯算法完成鸢尾花数据库的分类代码如下：

程序：鸢尾花贝叶斯

from sklearn import datasets

from sklearn.naive_bayes import Gaussian NB

iris=datasets.load_iris( )

X=iris.data

y=iris.target

from sklearn.model_selection import train_test_split

data_train，data_test，target_train，target_test=train_test_split(X，y)

bayes=Gaussian NB（ ） #生成

model=bayes.fit(data_train，target_train)

pred=model.predict(data_test)

error=pred-target_test

print(target_test)

print(error)

程序运行的结果如下：

[2 1 0 0 1 0 2 1 2 2 0 0 2 1 0 2 1 1 2 1 2 1 1 0 1 0 1 0 2 2 1 0 0 2 0 1 2 0]

[0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]

比较支持向量机的结果，朴素贝叶斯的分类结果也很好。