支持向量机（Support Vector Machine，SVM）由Cortes和Vapnik于1995年首先提出，在求解小样本、非线性、高维空间模式识别问题中，表现出许多特有的优势。

SVM算法的基本原理是控制风险最小，也就是样本分类误判的风险最小。参见图8.4.1的分类问题。从图中可以看出，可以找到多条直线将该两类问题有效分开。

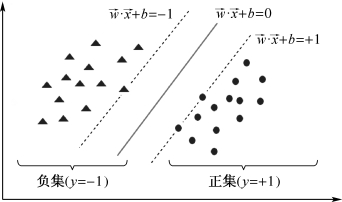
图8.4.1　两类问题分类svm示意图

但这么多解中，哪个解的风险最小？在很多算法中，采用所有样本参与建模评估来得到答案。而SVM采用分类边界上的样本，称为支持向量，通过这些支持向量确定最佳分割线。

sklearn库中提供的svm子集包含了多种支持向量机算法的实现方案。从大类上分，svm将问题分成两类：模式分类及回归建模。对分类问题，使用的SVC；对回归建模预测问题，使用SVR。具体算法特性及使用方法，请参阅网上相关文档。

【例8.4.1】 鸢尾花数据集在8.2.9节中已有介绍，采用sklearn提供的交叉验证方法，将数据集随机分割成两部分：训练集和验证集。用SVC算法建模并预报，程序的代码如下：

程序：鸢尾花支持向量机

程序执行的结果为：

[2 1 1 0 0 2 0 1 0 2 2 1 1 2 0 1 2 2 0 0 1 2 0 1 1 2 1 0 0 2 0 0 2 1 2 2 0 1]

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]

结果的第一行，是测试集的原值，第二行是对测试集的预报误差，结果全为0，说明没有误判。

【例8.4.2】 采用n份交叉验证策略对鸢尾花数据集建模。n份交叉验证建模，通过k Fold实现，其实现代码如下：

程序：鸢尾花支持向量机—交叉验证

程序执行过程中对每份验证样本预测，其结果如下：

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]

[0 0 1 0 0 0 0 0 1 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]

[0-1 0 0 0 0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0-1 0 0 0 0 0 0-1 0]

[0 0 0-1 0 0 0 0 0 0 0 0 0 0 0]

用n份交叉验证，建模者可以从每份预测样本的预测值对整个模型进行评估，均衡性比较好。

实际应用中，根据处理问题类型的不同，可以采用不同的向量机模型。对线性可分问题，使用线性模型，非线性分类，则可以采用非线性模型。如下面的两条语句，分别调用了不同的线性和非线性SVM模型。

svm=svm.SVC（kernel=ˈlinearˈ） #线性模型

svm=svm.SVC（kernel=ˈrbfˈ） #非线性模型

【例8.4.3】 股票交易中心每日都会产生与股价相关的大量数据，日积月累，变成数据的海洋，这其中自然隐含着某些规律。这里以沪市50ETF为例，下载其开市以来所有的周K线数据，如图8.4.2的Excel文件所示。

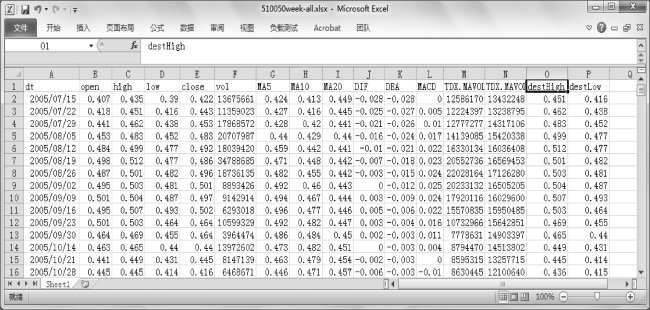
图8.4.2　A股50ETF周K数据

每个交易日的交易数据包括：开盘、最高、最低、各周期均线等。现在根据每天交易的信息，使用支持向量机方法建模，预测后续交易日指数的最高和最低位值。

对获取的excel文件，采用pandas将数据读入程序，考虑到不同的数据列数值量级差异很大，所以建模计算前，将其按列作数据预处理，将每列归为均值为0，方差为1。最后，将表的前13列作为自变量，最后两列作为函数展开建模。实现建模的Python代码如下：

程序：股票指数预测

import pandas as pd(www.daowen.com)

import numpy as np

data=pd.read_excel(r"E：\\00\\510050week-all.xlsx"，index_col=0，header=0)

#文件中，第一列为日期，第一行为标题，读取时予以指定

y High=np.array（data[ˈdest Highˈ]） #最高价格列，作为函数

y Low=np.array（data[ˈdest Lowˈ]） #最低价格列，作为函数

X=np.array(data)

X=X[：，：13] #数据的前13列作为自变量

std=X.std（axis=0） #取每列方差

mean=X.mean（axis=0） #每列的均值

X=X-mean #每列减去其均值

X=X/std #每列再除其方差

from sklearn import svm

from sklearn.model_selection import train_test_split

high X_train，high X_test，high Y_train，high Y_test=train_test_split（X，y High） #分割样本

svr=svm.NuSVR（kernel=ˈrbfˈ） #采用支持向量机回归算法

model High=svr.fit(high X_train，high Y_train)

pred High=model High.predict（high X_test） #预报测试集

error=（pred High-high Y_test）/high Y_test*100 #计算真值与预测值的误差

result High=np.c_[high Y_test，pred High，error]

print（"高位值预测结果"）

print(result High)

#对低位值建模

low X_train，low X_test，low Y_train，low Y_test=train_test_split（X，y Low） #分割样本

svr=svm.NuSVR(kernel=ˈrbfˈ)

model Low=svr.fit(low X_train，low Y_train)

pred Low=model Low.predict（low X_test） #预报测试集

error=(pred Low-low Y_test)/low Y_test*100

result Low=np.c_[low Y_test，pred Low，error]

print（"低位值预测结果"）

print(result Low)

程序在运行后，前几行的高位预测结果如下：

[[1.618 1.65159614 2.07639928]

[2.382 2.31447885 -2.83464114]

[1.399 1.43347895 2.46454284]

[1.703 1.66893212 -2.00046273]

[2.372 2.38187907 0.41648697]

[1.552 1.6198028 4.3687368]

[2.249 2.23597263 -0.57925156]]

结果中，第一列为真实值，第二列为预测值，第三列为百分误差。由于用于预测的数据都排除在建模数据外（独立测试），而预测的误差不大，说明建立的模型可以发现数据中的某些规律。机器学习是有效的规律发现过程，在数据量不断积累后，机器学习算法将更加体现其优势。