1.参数估算

参数估算指函数的形式已知，但函数中的一些参数有待通过实验测定的数据进行估算。scipy optimize包中的curve_fit函数，用来解决这类问题。

从最简单的直线关系方程y=ax+b入手，其中a、b为待估算的参数。

假设真实函数为y=2x+1，则首先产生自变量x的一系列采样点，并在这些采样点的函数值上增加一些随机噪声，得到一系列的点作为离散实验点（xi，yi）。在这些实验点的支持下，利用scipy optimize包中提供的curve_fit方法，求解系数a和b，典型的程序代码如下：

程序：曲线拟合

程序的执行结果如图8.3.6所示。

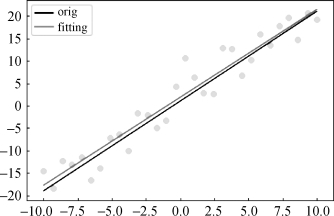
图8.3.6　y=2x+1函数的曲线模拟

curve_fit的输出结果中，popt列表包含每个参数的拟合值，此例求得的a为1.99022068，b为0.34002638。pcov列表的对角元素是每个参数的方差。通过方差，可以评判拟合的质量，方差越小，拟合越可靠。(www.daowen.com)

curve_fit方法可以用来求解任意复杂的参数估计，只要研究者有能力获得足够的实验点（xi，yi），且问题能给出函数的确切表达形式即可。

2.插值拟合

受多种因素（如费用和时间等）的影响，实验数据的获取很难做到采样间隔非常小。但采样点的多少，对进行其他计算如数值积分、趋势预测很有帮助。对这类问题，采用样条插值、线性插值、拉格朗日插值都是解决该类问题的算法，scipy的interpolate包可以很方便地完成这样的任务。

下面的代码是正弦波函数的插值模拟情况。首先在[0，2π]区间里等间距产生了10个采样点，计算其sin值并加10%的噪声，作为模拟试验采集得到的10个点。然后利用这10个点，采用线性、两次样条、三次样条插值函数插值拟合原函数sin（x）。程序的代码如下：

程序：样条插值拟合

程序运行的结果如图8.3.7所示。

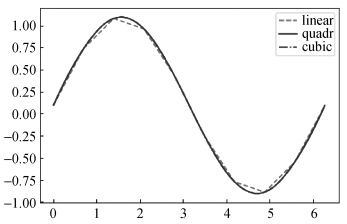
图8.3.7　采用线性、二次及三次样条插值模拟sin的结果

从计算得到的图形结果看出，针对sin原函数，采用二次样条插值所获得的模拟结果是最好的，即模拟得到的fq是最理想的拟合函数。

读者可以尝试修改采样点的数目，再重新运行程序，查看插值与原函数的相似程度。可以发现，采样点越密集，插值效果就会越好。