1.代数方程求根

高次代数方程求根，可以转化为优化问题，因此也可以使用optimize包求解。该包中的fsolve函数，从用户指定的起点开始，寻找f（x）=0时x的值，即方程的根。

下面代码是求解函数y=x2+20sin（x）的根程序。该函数在[-20，20]区间内的曲线如图8.3.5所示，它有多个根。使用fsolve函数求其根的代码如下：

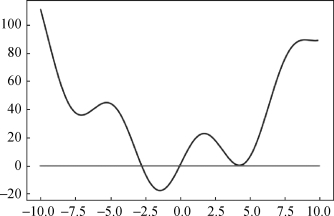
图8.3.5　函数y=x2+20sin（x）曲线

程序的运行结果如下：

[-2.75294663]

从-4出发，它找到了左侧的一个根。

改变优化的起始点，将程序语句修改如下：

ans=optimize.fsolve(f，1)

程序的运行结果为：

[0.]

它找到了右侧的根。说明初值的不同，所求答案是不同的。因此对该类问题，需要从不同的初值进行尝试。

3.2.3节中我们用二分法求解了0.01 mol/L的醋酸溶液的氢离子的浓度，其问题的实质是求解了一个一元三次方程的根，因而也可以使用optimize.fsolve函数求解，下面就是其代码：

程序运行的结果为：[0.00051122]，与3.2.3节我们自己编写的二分法所求结果一致。

2.代数方程组求解

scipy.optimize的fsolve函数的另一个更强大的功能是求解方程组。求解时，只需将方程组的右边全部规划为0，写成如下的格式：(www.daowen.com)

f1(x1，x2，…，xn)=0

f2(x1，x2，…，xn)=0

然后将上述的方程组定义为如下格式的Python函数：

def f(x)：

x1，x2，…，xn=x

return[f1(x1，x2，…，xn)，f2(x1，x2，…，xn)，….]

上面函数的实质，是将一组x的值，传递给函数，并立即解包成多维空间中的各个分量，利用这些分量表达每个方程，将方程的值形成一个列表，将该列表作为函数的优化目标，当每个函数的取值都为0时，就达到了优化的目的。

如对于如下的非线性方程组：

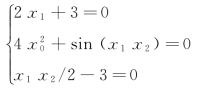
按前述规则，可以将求解代码编写如下：

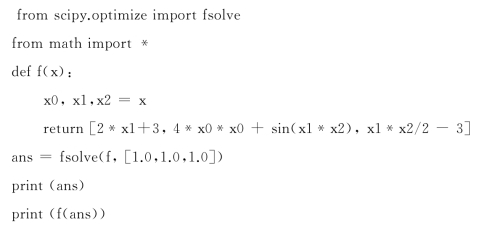
程序：非线性方程组求解

程序的运行结果如下：

[-0.26429884 -1.5 -4.]

[0.0,1.1482453876610066e-10,6.4002136923591024e-12]

即x0=-0.26429884，x1=-1.5，x2=-4为方程组的解，将该解代入方程，可以检验三个方程的取值是0或接近0。