寻优是指从给定的函数中找出函数的极值及对应极值的自变量取值，根据问题的复杂度可将寻优分为多种情况。scipy.optimize包提供多种求极值的方案，包括极小值函数fmin，使用BFGS算法（有兴趣的读者可以去了解BFGS算法）的fmin_bfgs函数、指定优化区间的optimize.fminbound函数，通过网格搜索的函数brute等，使用时根据问题的复杂度而定。

使用scipy寻优时，在程序的开头对优化函数进行引用，如：

from scipy.optimize importfmin

上述语句引用了fmin函数。

1.单极值点函数

函数f（x）=x2-4×x+8的曲线如图8.3.1所示。在x=2的位置，函数有唯一最小值4。

该类问题比较简单，直接使用fmin函数，给定寻优起始点即可求解。下面代码对f（x）=x2-4×x+8寻优求解。

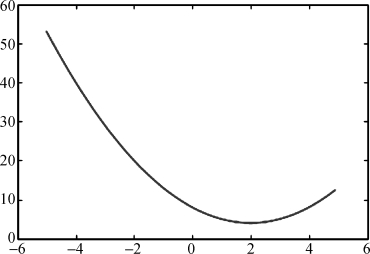
图8.3.1　函数f（x）=x2-4*x+8的曲线

【例8.3.1】 一维函数寻优

代码中先定义被寻优函数f（x），通过语句fmin（f，0）完成寻优。fmin函数的调用中，使用了f函数作为参数，后面的参数值0是指f函数寻优的起始点，因为函数f只有一个参数，所以只需写值0即可。

程序的运行结果如下：

即程序通过27次迭代，函数的最优值为4，最优值的位置为2，即x取值2时，达到了最优。

2.高维空间寻优

fmin支持高维空间的寻优，如函数：

z=x2+y2+8

其三维曲面图如图8.3.2所示，函数在x=0，y=0处有极小值。

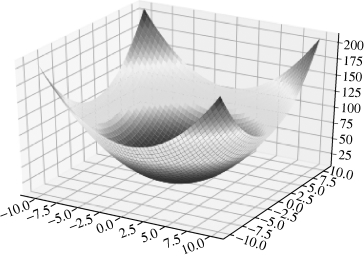
图8.3.2　函数z=x2+y2+8的曲面

fmin函数对高维空间的寻优，只支持单参数的传递方式，所以高维寻优函数的设计格式，其形参表需要使用元组传递多参数。

程序代码见例8.3.2。

【例8.3.2】 对两维函数z=x2+y2+8寻优

程序的执行结果如下：

3.多极值点寻优

前面例子，函数都有唯一的全局最优解，所以寻优函数可以较方便地找到答案。但实际应用中，很多问题都存在着多个局部最优解和全局最优解的问题。该类问题的求解则与寻优的起始点有很大的关系。

函数y=x2+10 sin（x）在[-10，10]上的图形如图8.3.3所示。可以发现，函数有较多的极值，或者说，有局部最小值，也有全局最小值。该类函数的求解，往往需要将程序以不同的初值运行多次寻找答案。

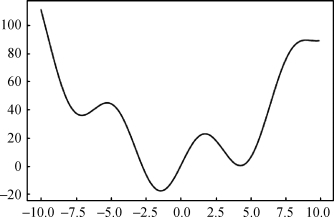
图8.3.3　函数y=x2+10 sin（x），存在多个最优解

【例8.3.3】 y=x2+20sin（x）寻优

通过上述代码寻优，得到的结果如下：

从程序的运行结果看，当起始点设置为0时，它找到了0附近（-1.42755178）的最小极值点-17.757257，该解也是全局最优解。

将寻优的起始点，从0变成5，即上述代码的寻优语句修改为：

ans=optimize.fmin_bfgs(f，5)

计算得到的结果如下：

程序只找到了5附近的局部最优解，并没有找到0附近的全局最优解。

4.区间寻找最优

求解全局最优点的一种替代方案是采用optimize.fminbound函数，它在用户指定的区间范围内，寻找全局最优点。如下面实例：

【例8.3.4】 求解y=x2+10 sin（x）的全局最优解

上述代码中，使用函数fminbound在[-100，100]区间范围内寻找全局最优点，得到的结果为：

-1.42755181859

可见，为了保证寻找到全局最优解，使用fminbound函数是一种不错的方案。(www.daowen.com)

5.指定网格寻优

scipy提供了一种在给定的网格点中求解全局最优的方案，其函数为optimize中的brute函数。首先看下面三维空间中的复杂函数。

z=sin(x)+0.05x2+sin(y)+0.05y2

为确切观察函数在三维空间的极值分布情况，先用如下的程序制作其三维曲面，代码如下：

程序的执行结果如图8.3.4所示。

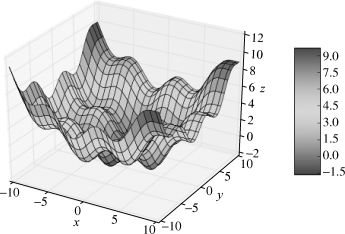
图8.3.4　三维空间含大量局部最优的问题

函数在整个实数域中存在大量的局部最优点。此类问题很难从某个出发点达到全局最优。针对该类问题，scipy提供的解决方案是：使用者提供全局寻优的网格点，通过网格搜索实现问题求解。

brute函数要求用户定义函数时使用一个参数。因此对多变量函数，可用tuple形式传送，所以函数的定义修改为：

import numpy as np

def f（p）：#用元组传递多维参数

x，y=p

ans=(np.sin(x)+0.05*x**2)+np.sin(y)+0.05*y**2

return ans

调用brute的求解代码如下：

import scipy.optimize as opt

rranges=（slice（-10，10，0.1），slice（-10，10，0.1）） #定义寻优网格点

res=opt.brute(f，rranges)

其网格定义的含义为：x和y都在-10，10区间内，采用步长0.1进行网格搜索求最优解。

6.条件约束的优化

实际优化问题，常会附加一些限制条件，此类问题就是有约束的优化问题。scipy的优化包optimize中提供的minimize函数，可以完成此类问题的求解。

使用minimize函数时，除提供优化函数本身外，还需要提供约束条件，通常以一组不等式表达；此外，还需要提供每个参数的优化范围。

如下面的问题：

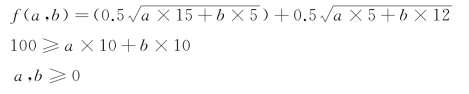
求函数f（a，b）在给定条件下的最大值。

因为minimize函数优化的是最小值，而上述问题求解的是最大值，所以在定义函数时，可以取函数的负值。而对条件及取值范围的限制，minimize函数分别用constraints和bounds参数决定。

如下面案例代码所示：

程序：条件优化

上述代码将参数a、b转化为一个列表，分别对应于x[0]和x[1]，这样便可以很方便地将优化问题推广到更多参数的优化，只需将后续参数再转化为x[2]、x[3]等等即可。

程序运行完毕后，result的运算结果为：

上述输出结果以一个字典的形式表达，其中最优位置为reslut[x]，其结果为array（[8.02547122，1.97452878]），即a=8.02547122，b=1.97452878为最优解。此时函数的最优值可以通过-result[ˈfunˈ]获取，其值为9.700883611487832。加负号的原因是函数的定义取了负数。

minimize函数有很多种调用形式，也支持多个限制条件。详细资料可以参阅http：//docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html。当出现多个限制条件时，需将每个限制条件整理成大于0的表达式，以一个字典的形式写进一个元组中，并赋值给minimize函数的constraint参数，例如下面的多条件限制问题：

min((x1-1)2+(x2-2.5)2)

x1-2x2+2≥0

-x1-2x2+6≥0

-x1+2x2+2≥0

有三个限制条件，因此需要定义三个表达函数。

程序代码为：

程序：多条件优化

res的结果为：