视频讲解：PCR算法原理

1.多元线性回归陷阱

在具体描述主成分回归之前，先回顾一下多元线性方程组的建模求解公式：

A=(XTX)-1XTY

在上述求解公式中，存在着矩阵求逆过程（XTX）-1，这是问题求解的关键因素。可以作这样的假设：如果X有n行m列，则XTX是m行m列的方阵。从线性代数的理论中可知，为使逆存在，XTX必须满秩。因矩阵X的秩最大只可能为n和m的小者，所以，要使XTX满秩，必须满足m<=n。

矩阵的组成中，以行代表样本，以列代表每个样本测量属性（自变量），则意味着，为使方程可解，参与实验的样本数，必须大于测量变量数，且样本间不线性相关。这一要求，在有些研究领域中容易满足，但也有些研究领域难以满足。例如，在中医药研发领域，以红外光谱测量样本的性质。此时，由于一个样本可以在非常多的波长下测量（变量很多），因此，从一个样本中，就可以测量到很多信息。此种情形意味着，实验样本难以准备（n小），而从样本中获取信息则变得容易（m大）。所以在形成的矩阵X中，m会远远大于n，从而导致A=（XTX）-1XTY无法求解，这就是多元线性回归在解决实际专业问题中存在的一些缺陷。

还有一种情形使得多元线性回归难以实现，即变量间的相关，它也会导致矩阵的逆不存在，使MLR建模失败。

2.主成分回归

在8.1.4主成分分析一节提到，PCA有能力获取矩阵中包含的独立信息，实现线性相关的信息合并，并且得分矩阵T是原矩阵在低维度的独立量张开的正交空间的线性变换。因此可以将前面多元线性回归的方程。

Y=XA

改写为：

Y=TA

因为建立回归模型前，已经对原始矩阵X进行了PCA分解，并使用得分矩阵T代替原始矩阵X参与回归，故被称为主成分回归（Principle Component Regression，PCR）。

由此求解回归系数A如下：

A=(TTT)-1TTY

T是列正交的矩阵，且只取了原始矩阵的独立信息而去除了线性相关部分，所以（TTT）-1必定存在，从而保证方程有解。

在求得A后，由于T=XP，所以原始表达式可改写成：

Y=TA=XPA=X(PA)=XC

记录最终得到的系数矩阵C，对未知函数值的测量矩阵Xnew，可直接对其预报如下：

Ynew=XnewC

3.主成分回归程序

从前面的原理描述中可以发现，主成分回归可以分为两个步骤，第一步是对自变量矩阵进行主成分分解，得到得分矩阵T，这可以借助numpy的SVD分解完成；第二步是得分矩阵T与函数的多元线性回归，可用MLR类实现。

PCA类接受传递进来的矩阵X，分解得到得分T和载荷P，代码存储在PCA.py文件中，定义如下：

视频讲解：PCR算法程序

程序：PCA

上面PCA类中，SVDdecompose方法返回一个列表，它记录了矩阵相邻奇异值的比值。通过它，可以有效地判别独立信息数（即主成分数）k。在确定k的前提下，可以继续调用PCAdecompose方法获得由独立信息组成的得分矩阵T和载荷矩阵P。

在PCA类、MLR类的支持下，编写主成分回归PCR类如下（存储在文件PCR.py）：

程序：PCR

PCR类的confirm PCs方法，调用了PCA类的SVDdecompose方法，以确定主成分数；model方法利用确定的主成分数，获取得分矩阵T和载荷矩阵P，然后用T和Y，调用MLR类建模，求得回归系数A。最后，为PCR类编写了predict方法，用于对未知样本进行预测，得到未知样本的函数值。

4.案例：主成分回归用于光谱定量分析

某同学在进行色素实验时，配置了6个三种色素（日落黄、柠檬黄、胭脂红）的混合物溶液，并在18个波长下测定这6个混合物的紫外光吸收值，测得数据及混合物的浓度分别存放在两个文本文件中，数据如图8.1.6所示：

视频讲解：PCR算法应用

程序：光谱PCR

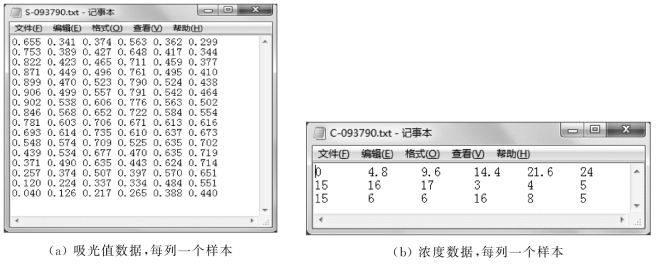
图8.1.6　色素混合物的吸光值和对应混合物浓度数据

根据朗伯-比尔定律，浓度与吸光值为线性关系。但由于所测数据矩阵有6个独立样本，18个测量量，因而不适合使用多元线性回归求解，请调用PCR类，编程求解模型的回归系数。

解：调用前面编写的PCR类，求解的程序代码如下：

import numpy as np

from PCR import PCR

S=np.loadtxt("E：\teach\Python\S-093790.txt")

S=S.T

#转置的原因是原始数据中，以列为单位保存数据，而PCR计算时，采用行为单位，即一行一个样本

C=np.loadtxt("E：\teach\Python\C-093790.txt")

C=C.T(www.daowen.com)

#C转置的原因同S

pcr=PCR(S，C)

print（"相邻奇异值比值"）

compare=pcr.confirmPCs( )

print（compare） #输出相邻奇异值的比值

k=int（input（"确定主成分数："））

pcr.model(k)

#建立模型

print（"回归系数"，pcr.A）

ans=pcr.predict(S)

print（"自身预报结果"，ans）

程序的运行结果如下：

在程序输出“相邻奇异值比值”后，可以发现第三个值为101，是一个突跃点。由此可以确定体系中的独立信息为3（对应于体系中有3种物质）。所以取3个主成分进行建模，并输出了模型的回归系数。为检验模型的可靠度，程序用建立的模型对自身进行了预报，将预报结果对照图8.1.6（b）的浓度数据（两者存在一个转置），可以发现数据中存在着一定的误差。

5.金融指数回归分析

本节采用互联网金融大数据，利用pandas的建模分析方法，建立上证指数与指数基金股价的回归分析，操作如下：

从证券网上交易系统（可从证券网站免费下载）下载上证指数（编号999999）所有日线交易数据，再下载50ETF指数基金的所有日线交易数据，以excel文件格式存储。打开下载后的文件，保留其基础数据，存储为csv格式。得到的结果文件截图如图8.1.7所示：

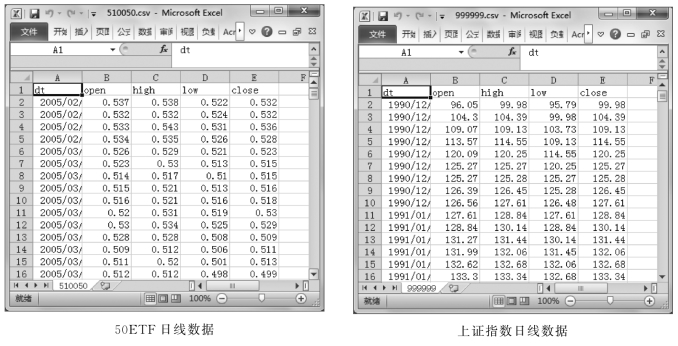
图8.1.7　从证券网站下载得到的上证指数和50etf数据

我们的目的是利用pandas的数据处理功能，考察两个指数日线收益率之间的关系是否符合线性。

从图8.1.7中看到，由于指数基金建立的日期较晚，所以两者之间的日期不对应，上证是从1990年开始，而50ETF则是从2005年开始，因此，需要将两者的日期统一起来。利用pandas的join函数，可以完成日期对齐的任务。见下面代码：

程序：股票指数收益率

import pandas as pd

import datetime as dt

import numpy as np

import matplotlib.pylab as plt

sh999999=pd.read_csv(r"E：\00\999999.csv"，index_col=0，header=0，parse_dates=True，sep=ˈ，ˈ，dayfirst=True)

data=pd.DataFrame({ˈszˈ：sh999999[ˈcloseˈ][sh999999.index＞dt.datetime(2005，2，22)]})

etf=pd.read_csv(r"E：\00\510050.csv"，index_col=0，header=0，parse_dates=True，sep=ˈ，ˈ，dayfirst=True)

data=data.join(pd.DataFrame({ˈetfˈ：etf[ˈcloseˈ][etf.index＞dt.datetime(2005，2，22)]}))

#通过上述代码，data中的两列数据分别是同一日期中上证和50etf的收盘价。

#现在可以考察两个收益率之间是否有线性关系，可以用下面的代码实现：

rets=np.log（data/data.shift（1））#计算收益率，以当日收盘价/前日收盘价计算

xdat=rets[ˈszˈ]

ydat=rets[ˈetfˈ]

model=pd.ols(y=ydat，x=xdat)

print(ˈmodel\nˈ，model.beta)

plt.plot(xdat，ydat，ˈr.ˈ)

ax=plt.axis( )

x=np.linspace(ax[0]，ax[1]+0.01)

plt.plot(x，model.beta[1]+model.beta[0]*x，ˈbˈ，lw=2)

plt.grid(True)

plt.axis(ˈtightˈ)

plt.xlabel(ˈshaihai stock indexˈ)

plt.ylabel(ˈ50etf returnsˈ)

plt.show( )

程序的执行结果如下：

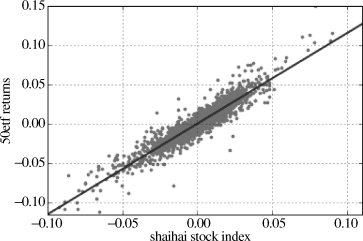
其斜率为1.150129，截距为0.000162。所得图形如图8.1.8所示，从图中可以看出，两者之间确实有线性关系。

图8.1.8　对数收益率散点图和回归直线