视频讲解：线性回归模型的矩阵运算规则

很多学科都有建模需求，以验证某种科学规律。这些科学规律，有一部分符合线性模型，可以表达为如下方程：

y=a0+a1x1+…+aixi+…anxn

当我们通过一些科学试验，得到了一组y和对应的xi值之后，接下来的任务是求取系数ai。该类问题就是线性建模。

1.一元线性回归

一元线性回归模型可以用下述方程表达：

y=a0+a1x

视频讲解：一元线性回归

当经过实验测定了n个实验点（xi，yi）后，在Excel中，通过制作“散点图”并模拟线性趋势，可以很容易求解出一条直线方程。

二维空间中的两个点可唯一决定一条直线。上述问题中，当实验点多于两个时，对直线拟合方程的求解就变成了一个优化问题，其准则是优化参数a0和a1，使得通过拟合的直线方程预测的值与实验值y间的差异平方和最小，即满足：

根据高等数学中的极值理论，可将上式分别对a1和a0求偏导，得到两个偏微分方程，并令偏导数为0，如下式所示：

上述两式可约简为：

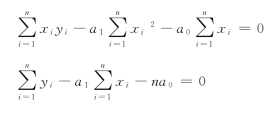
联合上述两式即可求得参数a0和a1。

上述简单的一元线性回归也可以表达成矩阵的形式如下：

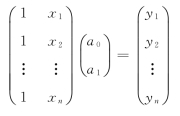
或写成

y=Xa

因此可以采用矩阵运算的理论求解系数向量a如下：

a=(XTX)-1XTy

在实际编程实现中，根据numpy提供的矩阵计算类库，采用矩阵运算求解通用性更好，因为它和多元线性回归的求解是一致的。

2.多元线性回归

视频讲解：多元线性回归MLR

多元线性回归指的是受多个变量线性影响的多个函数，形成一组线性方程，可表达如下：

其中y1，y2，…，ym是m个随变量x1，x2，…，xn变化的函数。

假设进行了k次实验，第i次实验时，变量x1，x2，…，xn的取值为x1i，x2i，…，xni，而m个函数y1，y2，…，ym的取值分别为y1i，y2i，…，ymi。则可以将k次实验的数据按函数公式写成如下的矩阵形式：

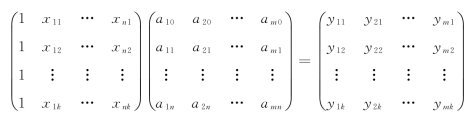
用矩阵形式表达如下：

Y=XA

因此，系数矩阵A求解公式如下：

A=(XTX)-1XTY

所以，通过比较，如果将向量看作是只有一行（列）的矩阵，则一元线性回归和多元线性回归是一致的。

在求得系数矩阵A之后，对于新的测量矩阵X，其预测结果可以按下面公式计算：

Ynew=XnewA

3.数据模拟方法

数据模拟在Excel中很容易实现，可在Excel中用随机数来完成这个任务。对一元线性方程

y=3.5+2.2x

产生模拟数据的具体操作如下：

设定A、B两列的第一行标题为x、y，然后在A2单元格中输入：=10*rand（ ），在B2单元格中输入：=3.5+2.2*A2+RAND（ ）/5。

其中B列的最后项rand（ ）/5，负责给模拟的数据添加适量的噪声。操作如图8.1.2所示：

图8.1.2　模拟的一元线性回归数据及其趋势线

将x列和y列的数据同时选中，以值拷贝的形式，拷贝到excel的其他sheet中，然后在新sheet中，再分别将x列和y列拷贝到磁盘文件1x.txt和1y.txt文件中。如图8.1.3所示。

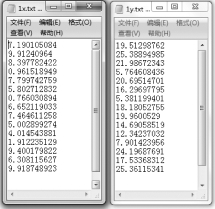
图8.1.3　模拟的一元线性回归数据整理为文件

多元线性数据的模拟可采用同样的思路，例如模拟线性方程组：

y1=1.2 x1+0.9 x2+3.3 x3

y2=0.7 x1+1.8 x2+2.3 x3

y3=0.4 x1+0.7 x2+4.9 x3

选定A、B、C列分别存储x1、x2、x3，该3列全部采用公式：=10*RAND（ ）产生随机数；然后采用上述方程组公式，分别在E、F、G三列产生y1、y2、y3的模拟数据，数据中可适当加入噪声，噪声的规模在10%以内，保证计算时线性关系不被破坏。如图8.1.4 Excel中产生的数据。

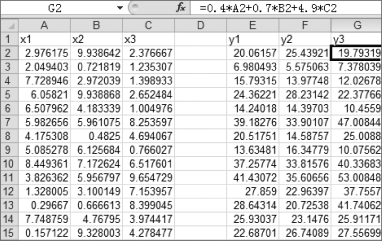
图8.1.4　线性方程组的模拟数据

从模拟得到的数据数量级看（y1，y2，y3），在每列的公式中增加一项rand（ ）是合适的（rand的量级为10-1），如修改为，y3=0.4*A2+0.7*B2+4.9*C2+Rand（ ），其误差应该在5%以内。

数据产生完毕后，按一元线性回归中所述的方法将数据分别拷贝到两个文件中，命名为mx.txt和my.txt中，如图8.1.5所示。

图8.1.5　Excel中模拟的数据形成文本数据文件

有了建模的数据文件后，可以尝试用numpy库求解对应的回归系数。

4.利用numpy求解线性回归

根据线性回归的求解公式，利用numpy求解多元线性回归方程的思路可描述如下：

①读入矩阵X；

②读入矩阵Y；

③利用A=（XTX）-1XTY计算系数矩阵A。(www.daowen.com)

设X、Y矩阵分别存放在C：\mx.txt和C：\my.txt文件中，Python程序代码如下：

import numpy as np

#从文件读取，获得X、Y矩阵

X=np.loadtxt(r"c：\mx.txt")

Y=np.loadtxt(r"c：\my.txt")

oneCol=np.ones(X.shape[0])

X=np.c_[oneCol，X] #将原来的X加一列，元素都是1，以求截距

#按A=（XTX）-1XTY求解

Xt=X.T

Xt X=Xt.dot(X)

inv=np.linalg.inv(Xt X)

temp=inv.dot(Xt)

a=temp.dot(Y)

print(a.round(4))

程序的运行结果如下：

[[0.-0.-0.]

[1.1 0.7 0.4]

[0.9 1.8 0.7]

[3.3 2.3 4.9]]

对照前面模拟过程给定的方程组，可以发现程序输出的第一列，正是函数y1的方程，后续依次对应y2和y3。由于3个方程的截距都为0，所以输出的第一行全为0。

可以采用面向对象的编程方法，在X、Y矩阵已知的情况下，将多元线性回归编写成一个类MLR，存储在MLR.py文件中，类代码如下：

程序：MLR

调用上述MLR类的主程序代码如下：

import numpy as np

from MLR import MLR

X=np.loadtxt("c：\mx.txt")

oneCol=np.ones(X.shape[0])

X=np.c_[oneCol，X] #将原来的X加一列，元素都是1，以求截距

Y=np.loadtxt("c：\my.txt")

mlr=MLR(X，Y)

mlr.fit( )

mlr.outputCoef( )

5.灰色系统预测GM（1，1）模型

视频讲解：灰色系统预测GM（1，1）模型的MLR求解

灰色系统是指系统的部分信息已知道，但又有一些未知的信息，在科学研究中最常见。灰色系统的预测则是指在已有经验的基础上，对系统将来的发展做出预测的过程，其中灰色预测模型GM（1，1）是被普遍认可的关于一个变量、一阶微分的模型。

GM（1，1）灰色预测模型的原理及实现可以简单描述如下：

①设系统初态时，已知原始数据序列如下：

x(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))

②将原始数据累加，消除或弱化随机干扰，得到新的数据序列：

x(1)=(x(1)(1)，x(1)(2)，…，x(1)(n))

其中新数据序列的每一项按下式计算：

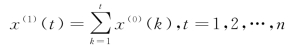
具体而言，新数据序列的每项是其前几项的累加和。

③依据序列x（1）建立一阶线性微分方程：

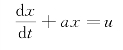
其中a和u分别称为发展系数和灰色作用量，为待求解的参数。

④GM（1，1）采用如下的方式求解参数a和u：

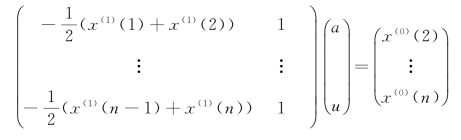
上式通过符号约定，可以简写为Ba=y。其中B为左侧的矩阵，向量a由参数a和u组成，y则是等式右边的向量。因为求导需要相邻的两项数据，所有等式右侧的向量从第二项开始。

这是一个多元线性回归问题，可以调用MLR类快速求解参数a和u。

⑤将求得的参数代入微分方程+ax=u，求解x，得到结果如下：

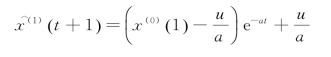
也就是说，对x（1）序列在（t+1）时刻的值的估计，可以通过x（0）序列及参数a和u完成。

案例：已知某公司2005—2014年的利润分别为（单位：元/年）：

（89677，99215，109655，120333，135823，159878，182321，209407，246619，300670），请预测该公司后续两年的利润。

根据GM（1，1）计算理论，编写Python程序如下：

程序：灰色系统预测

程序的运行结果如下：

[89677,89347,103393,119646,138454,160218,185405,214550,248277,287305,332469,384732]

即该公司后续两年的利润预测分别为：332469，384732。