视频讲解：PCA独立组分验证例子

矩阵的秩，对应于矩阵的独立信号源，如果可以分辨噪声，则矩阵的有效秩分析有其物理意义。这里以分析环境监控测量的仪器分析数据为例，通过SVD分解或主成分分析，求解其量测矩阵的有效秩数，以此来判断环境监测样品中的污染物数量。

图8.1.1是环境监测样本经过色谱—二极管阵列检测器获得的数据，经过excel制图所得的图形。

该数据是一个30×30的矩阵，可以通过下面代码，用SVD分解求取其所有的奇异值。

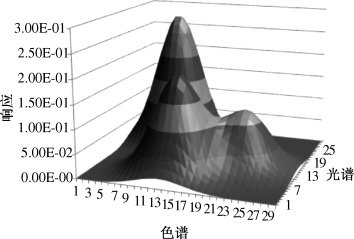
图8.1.1　环境监测数据的三维曲面图

import numpy as np

A=np.loadtxt("mix_2.txt")

B=np.linalg.svd(A)

lamda=B[1]

print(lamda)

程序运行结果如下：

[2.15161269e+00 1.05390680e+00 4.56283440e-01 1.66708386e-02

1.35967587e-02 1.24015141e-02 1.13980252e-02 1.10542845e-02

1.08529699e-02 1.04291078e-02 9.22815199e-03 8.70307124e-03

8.19399840e-03 8.02912448e-03 7.44376485e-03 7.10337395e-03(www.daowen.com)

6.25483051e-03 6.19978115e-03 5.31922925e-03 4.90022273e-03

4.68893146e-03 3.31606226e-03 3.27887784e-03 2.57445056e-03

2.16089683e-03 1.70161864e-03 1.29721798e-03 9.41540581e-04

5.50835995e-04 2.32174353e-05]

程序共求出30个奇异值。从这些奇异值中，很难一下子得出结论。但如果我们考虑到仪器信号测量的特点：实测信号是仪器响应与噪声的叠加，仪器响应信号应该远远大于噪声。由此，可以将相邻奇异值作比值运算处理：

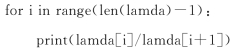
得到的结果如下：

2.04155877987 2.30976342916 27.3701551555 1.22608917534

1.09637892694 1.08804058552 1.03109570247 1.01854926428

1.04064222046 1.13014044457 1.06033281078 1.06212752528

1.02053448285 1.07863757637 1.04791960871 .13566210084

1.00887924103 1.16554125784 1.08550764826 1.04506171088

1.41400585676 1.01134059360 1.27362237837 1.19138059661

1.26990664935 1.31174457476 1.37776109026 1.70929385356

从相邻奇异值比值表中可以看到一个突跃点：27.37，它是第三/第四奇异值的比值。意味着：当提取了三个奇异值之后，后续的奇异值之间的大小相差很小，它符合随机噪声的规律。而该比值，正应该对应于仪器的信噪比，从而可以判断体系中有3种污染物质。